Let's try another, somewhat more difficult, volume example. In this example, we want to find the volume of a propane storage tank. This is a particularly important task including some details that are not purely mathematical, and there are some safety issues.
Propane storage tanks are an interesting technical challenge because propane wants to boil at normal environmental temperatures. The most efficient storage state for propane is as a liquid, and the only way to maintain its liquid state at room temperature is to keep it under pressure.
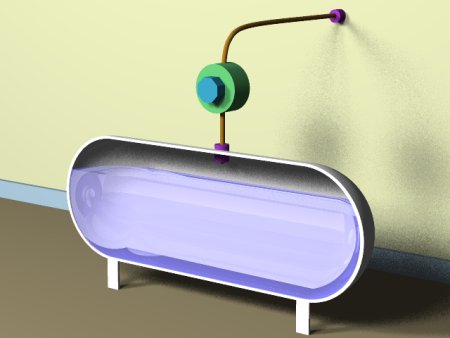
Propane tank cutaway view
|
|
In order to avoid the risk of bursting the tank as a result of temperature changes that expand the propane's relatively incompressible liquid phase, the tank may not be filled beyond 80% of its full capacity. Our task is to create a mathematical treatment for a typical propane tank — we need to determine its full volume, and we need to determine an 80% capacity point, to allow safe use of the tank in widely varying environmental temperatures. If we fail in our mission, someone will get blown up, so we need to be rigorous and careful with this problem.
All right. That should take care of those few who may think Calculus is always an esoteric pursuit with no real-world consequences. That is only sometimes true.
Remember from our previous volume examples that we can integrate to acquire a line from a point, a surface from a line, and a volume from a surface. That is exactly the approach we will use here.
Look at the graphic image on this page. Remember when we solve a problem of this kind, we want to "divide and conquer" — we want to evaluate the problem as a set of individual, manageable sub-problems. Using that philosophy, we see that the storage tank consists of three zones:
- A half-sphere at the left,
- A cylinder in the middle,
- Another half-sphere at the right.
We solved a sphere volume problem in the previous page and we can use that solution for the spherical part of this example. As to the cylindrical section of the tank, let's think about this. A cylinder's volume is equal to:
(1)
v = π r2 h
Where
r is the cylinder radius and
h is the cylinder height. But we can't apply this equation directly because our cylinder is lying on its side and it is only partly filled with liquid. So we should adopt the approach we have been using in previous problems — we want to imagine a point
y that is ascending through the tank. For this point, and as a first step, we want to acquire the width of a rectangular slice of the tank. We previously introduced a simple equation that will produce a half-circle for input arguments between -1 and 1:
|
(2)
|
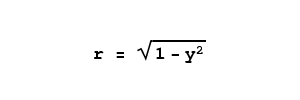
|
If we can find the rectangle's width for any
y height argument, we can then multiply by the rectangle's length to get an area, then integrate all the area results to acquire a volume. We can use a version of equation 2 to find a tank width for a given
y argument like this:
|
(3)
|
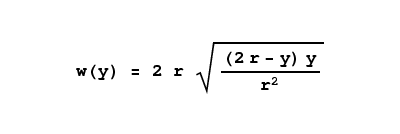 |
Function 3 provides the width for a given rectangle within the horizontal cylinder at height y, while the argument r represents the tank's radius. Then to get the surface area for each rectangle we multiply width by length. Having done this, we need to integrate the rectangles produced in equation 3 to get a volume for a given height:
|
(4)
|
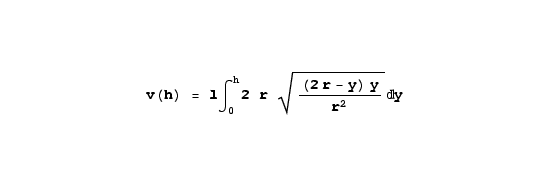
|
Where
l, lowercase L, is the length of the rectangles. The solution for integral 4 is:
|
(5)
|
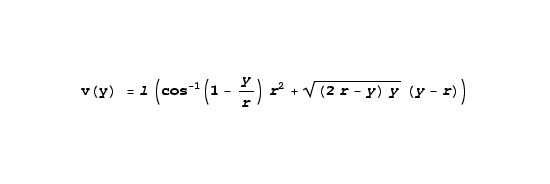
|
To include the spherical parts at the ends of of our tank, we had previously solved the problem of determining the partial volume of a sphere for a given height y within the sphere:
|
(6)
|
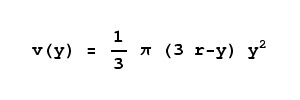
|
For the present problem, we should realize there are two half-spheres, one at each end of the storage tank, so we can use equation 6 for the spherical areas of the tank, then add this to our solution in equation 5 for the cylinder between the half-spheres, creating this combined equation:
|
(7)
|
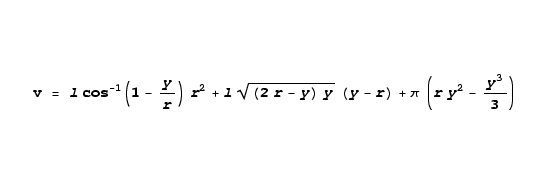
|
This is a rather complex equation and since there are safety issues involved, we should check our work. First, let's compare the results from equation 7 to the sum of the conventional spherical and cylindrical volume equations, remembering we can apply these two equations for the full volume case for a given tank radius
r and cylinder length
l:
| (8) v = | 4 | π r3 + π r2 l |
 |
| 3 |
For a tank with a length of 32 units and a radius of 4 units, equation 8 produces a result of 1792 π / 3 (1876.58...) cubic units. Our result shown as equation 7 produces the same result if we apply the argument
y = 2r, so our result has passed one test.
There is another test we can perform, one based on common sense. Because we evaluate the tank's volume by taking horizontal slices, we can see there is little volume at the bottom and top of the height variable's range, and more in the middle of the range. If we plot equation 7 against the height in the tank, we should see an s-shaped curve with little volume change near the ends of the range of height values, and large volume changes in the middle range. Such a graph appears on this page and it confirms our assumption, so our result has passed another test.
Finally, in connection with determining the 80% volume safe fill point, we would like to be able to acquire an internal liquid height for a given volume argument. Unfortunately, because of the complexity of equation 7 (in particular because of the appearance of the dependent variable
y both inside and outside the cos
-1 function), creating a suitable form that produces a height for a volume is not practical. This means we must rely on yet another numerical method, this one called "root finding."
One can perform a primitive kind of root finding with pencil and paper, and there are many computer programs used in mathematics that include root finders. Even spreadsheet programs of recent vintage possess this ability (usually a feature called "goal seek"). In essence, a root-finding approach for this problem would interpret equation 7 as a volume function
v = f(y) and ask "if v = 80% of full, what does y equal?"
For our example values above, a tank with a radius of 4 and a length of 32, the full volume is
1792 π / 3 or roughly 1876.58. 80% of this is about 1501.26. We can test
y values manually to produce an acceptable result, or we can submit the problem to a root finder to discover that the corresponding
y value should be about 5.927 height units.
This example is significant for producing a result too complex to allow easy conversion into other forms. We found that we had to use numerical methods to acquire certain kinds of results, even though the problem itself yields a closed-form solution. There are many such real-world Calculus problems.


 Share This Page
Share This Page

 Share This Page
Share This Page
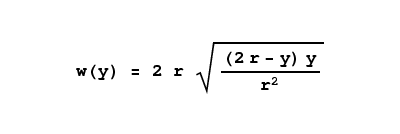
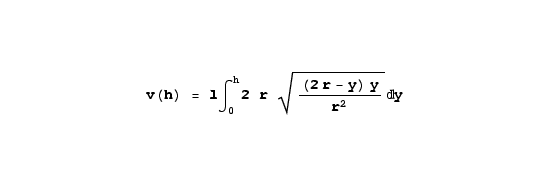
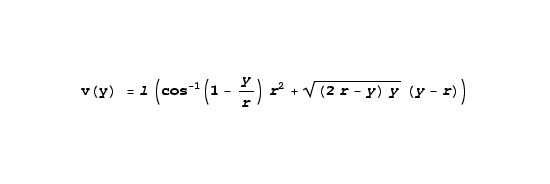
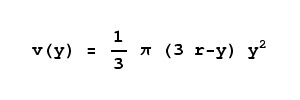
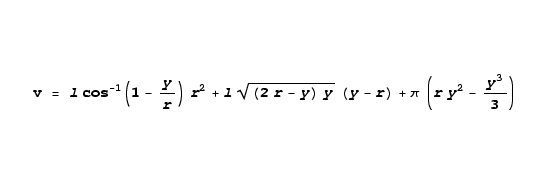



 Share This Page
Share This Page