Having covered the basics, we will now address some practical problems. In our prior examples, derivation and integration were always carried out with respect to time, but this is coincidental. Calculus problems can take many forms, they are by no means limited to time and motion studies.

Wine glass example 1
|

Wine glass example 2
|
|
Wine Glass 1
In this example we will compute the volume of a wine glass. Our first example glass is an inverted cone, shown as "example 1" on this page. How shall we proceed?
Let's break the problem down into sections. First, remember when one integrates during a problem involving physical dimensions, one typically adds a dimension for each integration. Integrate a point to get a line, integrate a line to get a plane, integrate a plane to get a volume. This should be your first clue.
Let's start by imagining a vertical axis, call it
y, that has as its zero point the bottom of the cone inside the glass. Imagine a point represented by
y ascending vertically through the center of the cone. Each
y value greater than zero lies at the center of a disc that extends across the inside of the cone. Each disc is two-dimensional and therefore has an area. So here is a strategy for solving the problem:
- Work out a function of y that produces the area of these discs.
- Integrate all the disc areas to get the volume of the cone.
For a given glass, the sides of the cone move away from a particular
y value at a rate we shall designate as
s (slope), which means the radius of each imaginary disc is equal to
y times the
s value. We can say:
(1)
radius r = y s
For each such radius, there is a disc with an area equal to:
(2)
area a = π y2 s2
To get the cone's volume, all we need do is integrate all the intermediate disc area values between 0 and a particular height
h in the cone. Like this:
|
(3)
|
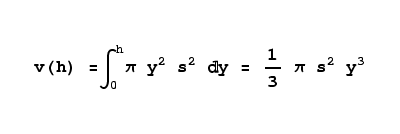 |
For a given glass, we would need to get a value for
s, the slope of the sides of the container. We can measure the height of the vertical axis to the rim (height
h), then the distance across the top of the rim (diameter
d). The second measurement
d may be divided by two to otain the radius
r at the rim, and our slope value
s would then be equal to
r/h.
Wine Glass 2
All right, we've computed the volume of one common wine glass shape. Here is another that is mathematically somewhat more interesting — it's a commonly seen wine glass in the shape of a sphere, cut off at the top. Once again, we need a function that will produce disc radii for y values.
For this problem, we would need to know the radius of the sphere represented by the wine glass interior volume. In solving a real-world problem like this, we would measure the interior of the wine glass at its widest point and divide by two to acquire the radius. This value is applied as
r in the equations below.
There is a relatively simple equation that creates a half-circle for an argument range between -1 and 1. This is ideal for our purpose, as we need to convert a vertical position within a sphere to a horizontal radius corresponding to that position. Here is the equation:
|
(4)
|
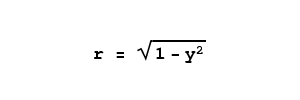
|
Remember for equation 4 that the
y values must lie between -1 and 1. For our disc area function, we need to enter the
y value corresponding to the vertical distance in the sphere represented by the interior of the wine glass, e.g. the equation must take into account the radius of the problem sphere, not a normalized value range as in equation 4, and further, it would be convenient if the
y value could range between 0 and the sphere's diameter. Here is the equation that accomplishes this, providing the area of the disc corresponding to the
y position within the sphere:
|
(5)
|
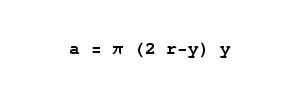
|
This equation accepts y values between 0 and 2r, the diameter of the sphere, and returns the area of the horizontal disc represented by that vertical y value.
Now that we have a suitable disc area equation, we can compute the volume by integrating the areas of the discs as in the previous problem. Here is the integral statement and its solution:
|
(6)
|
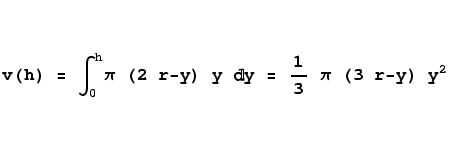
|
As a sanity check, let's find out if the result equation to the right above can compute the correct volume for a full sphere. We know that a sphere's volume is equal to
4/3 π r3. In this case, let's choose an
r value of 3 and a
y value of 6 (the sphere's complete diameter.
|
(7)
|
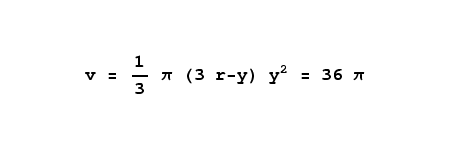
|
Yes, for a sphere with a radius of 3, 36 π is the correct volume. This means we can use this equation to say that, for a wine glass with an internal diameter of 9 centimeters (a radius of 4.5 centimeters) and a rim height of 6 centimeters, the volume is 282.74 cubic centimeters, a bit over 1/4 liter.


 Share This Page
Share This Page

 Share This Page
Share This Page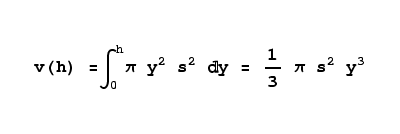
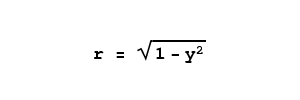
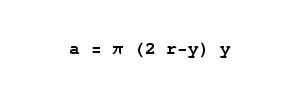
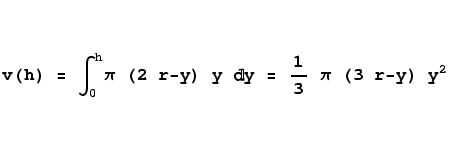
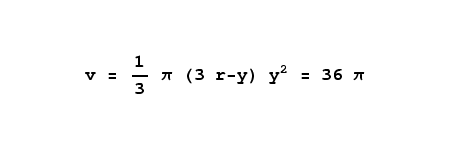


 Share This Page
Share This Page