When you visit a Web page, you expect it to cover one topic, without any egregious digressions or confusing side trips. I say this to warn you that this page breaks the rule, for an excellent reason — the three covered topics are interconnected in such a way that it's appropriate that they appear on the same page. I'll be talking about Olga Bay on Kodiak Island, how to compute bay tides and slack water, and the role of mathematics in people's lives. I assure you, it's well worth the voyage.
Olga bay is a nearly treeless region of Kodiak Island,
very pretty in its own way.
Olga Bay
After I turned around on the Alaska Peninsula (see previous page) and headed toward Kodiak Island, I had to make some quick decisions. Where should I go? I chose Olga Bay, the large bay at the south end of Kodiak Island — it looked like it would be interesting to explore by kayak. Then, having made that decision, a secondary issue was the choice of arrival time. I had read about Olga Bay that its entrance channel is long and narrow, and the currents are strong. I knew I should try for a time of slack water, easier said than done in a part of the world without much guidance that correlates ocean tides and times of slack water in bay entrances.
In my own defense, let me say that, for most of the crossing between the neighborhood of Cape Providence and Olga Bay the conditions were pretty rough, not a situation likely to produce much deep thought or reflection. I quickly ran through what I thought I knew about slack water times at bay entrances.
At Lituya Bay, a dramatic, somewhat risky bay between Cape Spencer and Yakutat, I had entered at the high or low tide times for the ocean outside the bay, "reasoning" that the slack water time would be more or less the same as the high or low tide time. But when I arrived, I noticed the local fishermen waiting until some time after those high and low tide times. I made a mental note to think about this later on.
At Princess Louisa Inlet in British Columbia, another place with dramatic, not to say dangerous, entrance currents, I had gotten various estimates of the slack water times, some from published tables, some from my own tide program
JTides. Obviously I believed my own program's prediction was more accurate than the published one, but the published one simply suggested waiting a certain number of minutes after high or low tide at a reference location near Vancouver! I thought this was simply a way to avoid having to acquire better information, but Princess Louisa Inlet is rather distant from the ocean, with a consequent amplification of all the confounding factors that can make tidal prediction difficult (changes in barometric pressure, winds, man-made changes in the landscape). And on numerous visits to Princess Louisa Inlet I noticed the actual on-scene slack water times were not predicted by either source with any great degree of accuracy.
But all this aside, I saw that the times of slack water were typically well after the time of high or low tide, as in 25 to 45 minutes. I initially attributed this to the site's distance from the ocean.
This was the fog of my thinking as I approached Olga Bay, having arranged to arrive only shortly after a high ocean tide, again "reasoning" that this would be a reasonable passage time. Imagine my surprise as my boat was bounced about in pretty strong currents (better than five knots) on the way into the bay. It was a fun ride, no serious risk, but I was rather disappointed in my entirely wrong estimate of arrival time and the reasoning I had used to come up with it.
So, in my humiliation at completely misjudging the arrival time, and now in the comparative shelter of the bay (no more tables rolling over), I began to seriously think about bay tides and the issue of slack water. Over a cup of tea, I asked myself what a bay is most like, expressed in the simplest physical terms. I imagined a bay being filled by the ocean through a narrow channel and I realized something that seems obvious once you think of it: the rate of water flow through the channel is proportional to the difference in water levels between the bay and the ocean — the greater the difference in water levels, the greater the rate of flow (within some practical limits). I know there's a popular name for such intellectual insights, but in this case the result was so obvious I decided to call it a "duh!" moment.
My next realization was that such an ocean+channel+bay system resembles many other natural systems where the rate of change is proportional to the difference between two quantities:
- In thermodynamics, the case of two thermally coupled bodies, where heat flows from a high-temperature body to a low-temperature body until the temperatures are equal, and the rate of heat flow is proportional to the difference in temperatures.
- In electronics, an RC (resistor-capacitor) circuit, where the electrical current through the resistor connected between a voltage source and a capacitor is proportional to the difference in voltage between the source and the capacitor.
- The case of two connected gas reservoirs, where the rate of gas flow is proportional to the difference in pressure, and the connection between this case and the much more general (and complex) case of weather systems that are governed by the same relationship — the greater the difference in pressure between a high-pressure and a low-pressure region, the greater the wind velocity betwen them.
So, in a matter of minutes, I had shaped a reasonable model for bay tides, and I had made an ironic connection between my model and the high wind velocity that had brought me to Olga Bay in the first place!
Tides in bays
Now, for the next step, what tool is appropriate to make a general statement about all these different kinds of physical systems (and many others not listed)? What technology can make a single, powerful statement that applies to all of them? I'll let the late Nobel Prizewinner Richard Feynman say it for me: "To those who do not know mathematics it is difficult to get across a real feeling as to the beauty, the deepest beauty of nature. ... If you want to learn about nature, to appreciate nature, it is necessary to understand the language that she speaks in." I couldn't have said it better.
Let's start with a simpler case and then work up to a reasonable tidal model. Let's consider the simple case in which a fixed quantity of something (electricity, water, gas, thermal energy) is being conducted through a path with some resistance to flow, and causing a secondary vessel to accumulate it. The following differential equation describes the relationship:
| (1) |
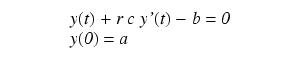
|
Where:
- y(t) = the value that is changing with respect to time (in our example, the bay's tidal height).
- y'(t) = the rate of change in y with respect to time (in our example, the current in the channel), or, more formally, the first derivative of y with respect to time.
- a = The initial value for y at time zero, or y(0).
- b = the final value for y at t = infinity.
- r = the channel's resistance to current flow.
- c = the bay's capacity (the volume of water that it can hold).
Those with a background in science or engineering will see that this equation is identical to that used in thermodynamics, electrical engineering, and many other fields, with appropriate changes in the meanings of R and C.
Here's the closed-form solution for equation (1) (a form with which we may obtain practical results):
| (2) |
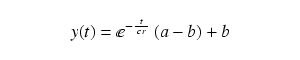
|
The peculiar-looking "e" above is the base of natural logarithms (2.71828...).
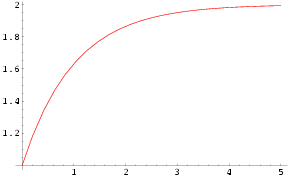
Here is a plot of equation (2) with typical values (a = 1, b = 2):
Notice about this plot that, as expected, the rate of change in y declines as the value of y approaches the final value. This is a very commonly seen graph in the study of natural systems.
The above plot is the water level change we would see in our imaginary bay if the bay were to be filled once by an equally imaginary ocean without tidal changes. But the ocean's tides are constantly changing, so we need a different equation to make it relevant to the bay tides problem. Let's say we have a sinusoidal tidal curve with the same amplitude on each tidal cycle (rarely true in reality, but a useful assumption for modeling tidal systems). Here is the new equation:
| (3) |
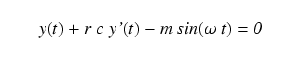
|
Where m = the ocean tidal magnitude, ω = 2 π f, and f = tidal frequency. Notice about equation (3) that there are no terms that cope with initial or final values — this is because tides are a continuous process, with no beginning or ending. Even though this equation differs from the first example, the rate of water flow remains proportional to the difference in tidal height between the bay (given by the "y(t)" term) and ocean (given by the "m sin(ω t)" term), the same basic idea as the first equation. What has changed is the driving waveform, now resembling an ocean tide.
And, as before, there is a practical solution for equation (3):
| (4) |
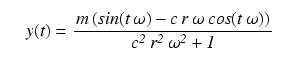
|
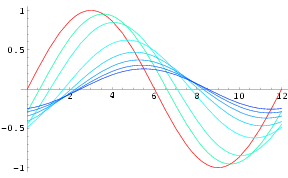
Here is a set of plots for equation (4):
The red plot line is a reference tidal waveform for the hypothetical ocean outside the bay, the green through blue plot lines are solutions for different bay capacities and/or channel resistances to water flow.
Notice the following points about this system:
- In the above graph, the slack water times occur when the example green and blue lines (bay water heights) cross the red line (ocean water height), which are the times when the ocean water height and the bay water height are equal. Notice that those are also the times of high and low tides in the bay (because that is when the channel current stops and reverses direction). Therefore, if you have the times of high and low tide inside the bay, these should also be the approximate times of slack water in the channel (disregarding confounding factors).
- As the bay's capacity increases (plots moving from green toward blue), the tidal range inside the bay decreases and the time delay for slack water increases. The relevant Coast Pilot entry for Olga Bay says that the tidal range inside the bay is quite small, as in 2-3 feet, therefore the slack water times occur long after the times of ocean high and low tides.
- Imagine a bay of infinite capacity. For such a bay, the tidal height inside the bay would not change, it would be equal to the average ocean tidal height, and the slack water times would be nearly three hours after high and low tides (on average).
- Imagine a bay with a small capacity, or one with little channel flow resistance. For this bay, the tidal height inside the bay would be nearly the same as the ocean height, and the slack water times would be only slightly delayed after the times of high and low tides.
Conclusions:
-
Slack water times in a bay channel take place virtually always after ocean high and low water times. Small bays or bays with large, wide entrance channels, will tend to show slack water times near the times of ocean high and low water. Larger bays or those with long, narrow entrance channels, will show larger time delays after high and low water times, sometimes approaching three hours after ocean high or low water on average.
-
As a bay's capacity increases (and/or as the entrance channel's resistance to flow increases), the slack water delay time after high and low tide gradually increases, to almost three hours for the largest bays with the smallest entrances. A primary clue that a bay will show a long slack water delay after high and low tide is the presence of relatively small tides inside the bay, compared to reference ocean tides outside the bay. Olga Bay is an example of a large bay with a small, meandering entrance, so it fits this profile, and has long time delays between ocean highs and lows and channel slack water.
|
Olga Bay is rather a special case even with this level of analysis, because it is fed by another bay (Moser Bay) with its own narrow entrance and time constant factors. Given this double-bay system, I wouldn't be surprised if Olga Bay slack water times were measured to be greater than three hours later than ocean high and low water times.
After performing the first version of this analysis within Olga Bay and paddling around in my kayak for a few days, I used the analysis results to choose a more appropriate departure time, and with a good outcome — almost no current in the channel.
Mathematics
To those trained in mathematics, in particular those with some physics training as well, the foregoing exposition will seem rather obvious, an easy-to-grasp analysis of a simple physical system — enlightening but not particularly challenging.
To those who do not understand mathematics, the entire preceding section may seem entirely mysterious, black magic. Some might even wonder if such mathematical knowledge is really necessary. Among Americans in particular, very few have the requisite training to follow the preceding section. That is because Americans are rapidly falling behind the rest of the world in many academic subjects, and science and mathematics are near the top of the list of "problem subjects" for American students.
Well, guess what? People who understand mathematics are more likely to understand the world around them, are more likely to be members of the teams that will build tomorrow's world, and colonize Mars.
In the future, to be blunt, those who don't understand mathematics will serve hamburgers to those who do. I would like to paint a rosier picture, but as time passes, as the requirement for more technical knowledge grows, people who do not understand mathematics will simply be unemployable.
I think the riskiest trend in a democracy is to accept the existence of a division between those who are educated well enough to function as citizens of the modern world and those who are not. Such a division is already apparent in the US — an increasingly smaller minority of educated people dispenses wisdom to an increasingly larger majority of technical illiterates. This makes "democracy" more a principle than a fact, because when the majority of citizens cannot comprehend the world around them, they also cannot function as citizens — instead of thinking for themselves, they allow themselves to be told what to think by "experts." This is dangerous and unacceptable.
Also, seemingly a well-kept secret, mathematics is personally enriching and fun. When I realized bay tides were governed by the same physical principles as many other parts of nature, such that the same differential equation could be applied to all of them, I found it a moving experience. Imagine a single equation that in large part describes such diverse topics as weather systems, heat flow, gas physics, tides and electronics. Then ... imagine not being able to understand the equation, or even the branch of mathematics it belongs to.


 Share This Page
Share This Page

 Share This Page
Share This Page

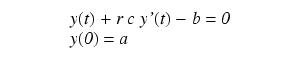
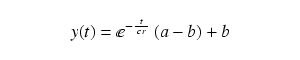
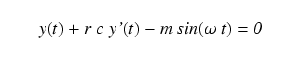
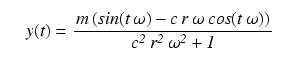


 Share This Page
Share This Page