

 Share This Page
Share This Page| Home | | Science | |  |  |  Share This Page Share This Page |
A comprehensive JavaScript/Canvas orbital physics model
— Copyright © 2013, P. Lutus — Message Page —
(double-click any word to see its definition)
This application is an interactive simulation of a solar system with planets, comets and a dark energy model. If you want to see the simulation in 3D, get some
anaglypic glasses and enable "Anaglyphic" below.
The display window allows mouse movements to control rotation (drag mouse cursor horizontally and vertically) and scale (spin the mouse wheel). This model is also mobile-aware, responding to touch where that is possible. One touch controls rotation much like a mouse cursor, two touches controls scale.
A full exposition of the physics and math appears below the simulation.
I once wrote an article set describing the physics of Dark Energy, a cosmological mystery that will eventually cause the universe to fly apart. To show how dark energy works I created a three-dimensional solar system model including a dark energy term that causes the model to become unstable. The dark energy level required to tear the solar system apart is much higher than exists in nature, but I wanted an easily understandable model for tutorial purposes.
I wrote my original solar system model in Java, because Java can be embedded in a Web page and Java runs reasonably fast. Since then several things have happened to make Java a bad choice for an embedded Web page application. One, the Java browser plugin has begun to have some serious security issues (this problem doesn't affect desktop Java applications, which are still secure). Two, a new way to present graphic content and animations in a Web page, based on the HTML5 canvas tag, has greatly improved. Three, browser JavaScript engines have become much faster and more powerful, allowing real-time animation speeds. Finally, in its newer browser versions Microsoft has come around to supporting the canvas tag and some of the newer JavaScript features this kind of simulation requires.
Combining ColorsComputer graphic colors are represented by numbers. An integer meant to represent a color has three parts, for red, green and blue. Expressed in hexadecimal, a color number looks like this: ffffff. In this scheme, there are 25510 (in hex, ff) shades of red, green and blue, for a total of 16,777,21510 distinct colors.
With a black background, if I want to produce white where red and cyan are both present, I need only combine the colors using a logical OR operation (symbol |). Red's number in hexadecimal is ff0000, and cyan is ffff. Using computer logic, ff0000 | ffff = ffffff or white (to test this idea on a decimal calculator, add 990000 to 9999). This is what the canvas "lighter" global composition operator does — by combining red and cyan to produce white, the anaglyphic effect is preserved.This project uses a JavaScript physics engine and a canvas-based display. For many years a browser-based JavaScript program couldn't run fast enough for something as demanding as a physics simulation, but in recent years browser designers have made great strides in speeding up their JavaScript engines, something I discovered by writing a computation-intensive Mandelbrot set generator that turns out to be remarkably fast on most platforms.
There are still some problems with the canvas-based display, most having to do with browser differences. I've always been a fan of anaglyphic 3D displays because the required equipment is so cheap and low-tech (a pair of red/cyan glasses is all you need). To create an anaglyphic image, you draw the image twice with a parallax angle separation between the renderings, an angle like a person has between his eyes. This produces two complete overlapped images, one red, one cyan. The 3D anaglyphic glasses separate the images, so the left eye gets the left image and the right eye gets the right image, and you experience a 3D effect.
Now for an important detail. If two areas of the anaglyphic image overlap, and both eyes should see brightness, the graphics rendering method needs to automatically produce an additive combination of red and cyan, i.e. white. This allows both the red and cyan anaglyphic lenses to accept that area as part of the image and support the effect. This result is achieved by choosing a canvas global composition method called "lighter", which means any new additions to the image are logically combined with what was there before, and combining red and cyan produces white (see "Combining Colors" on this page). All present browsers that support the canvas tag, also support the "lighter" composition operator.
But there's another anaglyphic display mode in which the background is white and the rendering is drawn in colors darker than the background. For this mode, when combining analgyphic colors, the opposite operation is required — an area having both red and cyan must become black. For that effect, we need a composition operator called (wait for it ...) "darker". As it turns out, some ill-informed people responsible for the HTML5 specification have decided to drop support for "darker". After all, we already have "lighter", and "darker" is like "lighter" but trivially different. Right?
Because "darker" was once part of the HTML5 canvas specification but is now being considered for elimination, the result is that different browser builders have begin moving in different directions, generally a bad thing. Google Chrome and Safari support "Darker", but Microsoft Internet Explorer and Firefox don't. The result is that the appearance of the inverted anaglyphic display above will depend on which browser you're using.
The Simulator
A multi-body Newtonian gravitation simulator is relatively easy to write in two or three dimensions. For a system with more than two interacting bodies, and because of the three-body problem which prevents a closed-form solution, such a system must be modeled numerically. As it happens, all multi-body gravitational simulations are, and must be, performed numerically — from the simplest computer games to galaxy evolution simulations running on supercomputers.
The simulator on this page models the primary bodies in the solar system, including Pluto (even though Pluto is no longer regarded as a planet), and a set of comets for realism.
A gravitational simulation sets initial conditions of position and velocity for all the modeled bodies, then the simulation commences using increments of time. In such a simulation, each modeled body retains state vectors for position and velocity whose initial values are modified over time:
- A radius between the gravitating bodies is computed: (1) $ r = \sqrt{x^2+y^2+z^2} $
- A gravitational force scalar is computed: (2) $ f = - \frac{G m_1 m_2}{r^2} $
A normalized direction vector (or unit vector) is computed to provide a direction for the gravitational force scalar: (3) $ \hat{r}\{x,y,z\} = \frac{\{x,y,z\}}{\sqrt{x^2+y^2+z^2}}$
- G = Universal gravitational constant
- m1 = mass of body 1
- m2 = mass of body 2
- r = radius obtained from equation (1)
- The velocity vector is updated by gravitational acceleration multiplied by the unit vector: (4) $ \vec{v}_{t+1} = \vec{v}_{t} + \hat{r} f \, \Delta t$
- The position vector is updated by velocity: (5) $ \vec{p}_{t+1} = \vec{p}_{t} + \vec{v}_{t+1} \, \Delta t$
- The updated position is plotted on an output device and the process is repeated.
When the above model is created in three dimensions as in the simulator on this page, there are some optimizations to avoid the use of inefficient trigonometric and other relatively slow functions that would reduce the frame rate. Here's a breakdown of one key optimization:
- The usual approach to creating a gravitational acceleration vector is to multiply a force scalar by a unit vector as shown above. Because this is the most complex part of the mathematics, it should be examined more closely.
- The force scalar looks like this (from equation 2 above): $f = - \frac{G m_1 m_2}{r^2}$
- The unit vector looks like this (equation 3 above): $ \hat{r}\{x,y,z\} = \frac{\{x,y,z\}}{\sqrt{x^2+y^2+z^2}}$
- In this expanded view of the unit vector, the three Cartesian components {x,y,z} are divided by a hypotenuse that represents their three-dimensional radial distance. The result is a vector in which each Cartesian component is a number 0 <= n <= 1 such that $ \sqrt{x^2+y^2+z^2} = 1$ (the normal meaning of "unit vector").
- Because the unit vector is multiplied by the force scalar to produce an acceleration vector $\vec{a}$, some optimizations are possible:
- Unit vector $ \hat{r} = \frac{1}{\sqrt{x^2+y^2+z^2}} = (x^2+y^2+z^2)^{-1/2}$
- Radius (equation 1) $ r = \sqrt{x^2+y^2+z^2} $
- Force scalar $f = - \frac{G m_1 m_2}{r^2} = - G m_1 m_2 \, (x^2+y^2+z^2)^{-1}$
- Acceleration vector (unit vector times force scalar):
$ \vec{a} = - G m_1 m_2 \, (x^2+y^2+z^2)^{-1} \, (x^2+y^2+z^2)^{-1/2}$- Combining terms:
$ \vec{a} = - G m_1 m_2 \, (x^2+y^2+z^2)^{-3/2}$- The result of this optimization is an acceleration vector that represents an absolute minimum of computation overhead and that accurately represents orbital gravitation in three dimensions.
Some Orbital Physics
A cornerstone of modern physics is the idea of energy conservation. While watching the orbits in the simulator, one might wonder whether they model reality and conserve energy. After all, the elliptical comet orbits seem to be speeding up and slowing down over time, and higher speed represents higher energy. How do they conserve energy?
To answer, we need to examine two aspects of an orbiting body — its velocity, and its distance from the parent body. Here are the equations:
- Kinetic energy: (7) $E_k = \frac{1}{2} m_1 v^2$
- Gravitational potential energy: (8) $E_p = - \frac{G m_1 m_2}{r}$
It can be seen that kinetic energy increases proportional to the square of velocity, and the gravitational potential energy result becomes more negative as an orbiting mass approaches its parent body. As it turns out, in a frictionless orbit, these two forms of energy always sum to a constant — no energy is gained or lost:
- Total of kinetic and potential energy: (9) $E_t = \frac{1}{2} m_1 v^2 - \frac{G m_1 m_2}{r} $
Models of this energy relationship — like this one — show that these two properties of orbits are perfectly balanced. What's interesting about this part of physics is that there are a number of results from the past, like Kepler's laws of planetary motion, that describe some things that (at that time) couldn't be explained — for example, "A line joining a planet and the Sun sweeps out equal areas during equal intervals of time".
It turns out that Kepler's laws describe properties of orbits that would have to be true if orbits conserved energy, but they were formulated long before people began thinking about energy conservation as a physical principle.
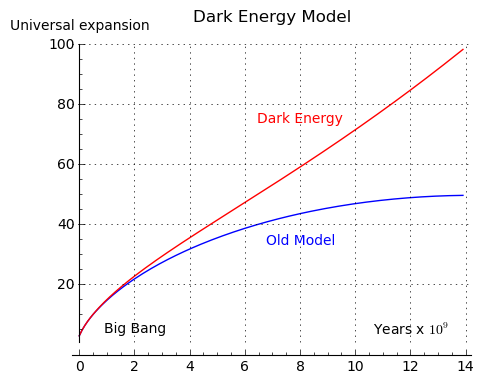
Dark Energy
The discovery of dark energy must rank as one of the biggest shocks to the world of physics in the last 100 years. According to some careful measurements followed by creative theorizing, dark energy is a weak repulsive energy field filling all of space. For masses in close proximity, it has negligible effects, but for masses more widely separated than galactic clusters, dark energy exerts a larger influence than gravity, gradually pushing masses father apart.
During the evolution of the universe from the Big Bang to the present, dark energy played no significant role until about 6 billion years after the Big Bang, or 7.7 billion years ago, at which point dark energy became a player in the universe's dynamics. In the long term, it is thought that dark energy will cause an exponential expansion of the universe's matter, which gives a final answer to the perennial cosmological question about the long-term fate of the universe (i.e. will the universe recollapse, gradually expand asymptotically, or expand without bound?).
The model built into this page can show my readers how dark energy would work if it were a great deal stronger than it is — it's just a demonstration of the effect, not its magnitude. Simply click the "Dark Energy" checkbox and see what happens to the orbiting masses. In reality, over a very long time, clusters of galaxies, not planets, would drift farther and farther apart, and the universe will gradually become a dark, nearly empty place.
The present mathematical model for dark energy is much like that suggested by Albert Einstein in 1917. Einstein had a purely theoretical reason for suggesting that dark energy might exist. Einstein was aware that the universe predicted by General Ralativity was unstable — under the influence of gravity, the universe would either fly apart or fall together, but could not be static. Because there was no evidence for either of these outcomes in 1917, Einstein introduced a constant term he called the "cosmological constant", whose purpose it was to resist the tendency of stationary masses to fall toward each other. Einstein believed his cosmological constant allowed a static universe to exist.
Within a few years, Edwin Hubble discovered the universe was expanding, which deprived the cosmological constant of a purpose. Also, as it turns out, the mechanism proposed by Einstein could not have balanced a static universe — it would have been like a pencil balanced on its tip. Einstein later called his cosmological constant "the biggest blunder in my career".
Interestingly, Einstein's original field equation included the cosmological constant this way:
(10) $ \displaystyle R_{uv} - \frac{1}{2}R \, g_{uv} + \Lambda \, g_{uv} = \frac{8 \pi G}{c^4} T_{uv}$Where $\Lambda$ is the cosmological constant term, located on the left-hand side of the field equation, grouped with terms that define spacetime curvature and geometry. In the new formulation, meant to address the dark energy issue, the constant term has migrated to the right-hand side of the field equation, grouped with terms having to do with mass/energy, unfortunately in a way that's difficult to summarize concisely.
In the very simple numerical model on this page, a dark energy term optionally modifies the gravitational force1 equation this way:
(11) $f = \Lambda - \frac{G m_1 m_2}{r^2}$Where $\Lambda$ has a small positive value. In thinking about this equation, it can be seen that, because the dark energy term is a constant, and because the gravitational force1 declines as the square of distance, the dark energy term has a much larger effect on widely separated masses than it does at close range.
Again, in this model, I have chosen a very high default value for dark energy, much higher than exists in nature, just to be able to show a dynamic effect on a short time scale and on the scale of the solar system, and to show the different effect dark energy has at short and long distances. In this artificial demonstration, when the dark energy option is activated, all the planets inside the orbit of Mars remain in stable orbits, the orbit of Mars itself becomes somewhat unstable, and all masses farther from the sun quickly depart the solar system.
Again, in reality, because of its small theorized repulsive force, real dark energy has little or no effect at scales smaller than galactic clusters, and the evolution of the universe under the influence of dark energy will require many billions of years, so I ask that my readers remember that this demonstration is not meant to reflect reality.
1: In General Relativity, gravitation is not a force, but results from spacetime curvature. Gravity can be modeled as though it is a force, but one must remember this is a convenient fiction.
| Home | | Science | |  |  |  Share This Page Share This Page |