

 Share This Page
Share This Page| Home | | Mathematics | |  |  |  Share This Page Share This Page |
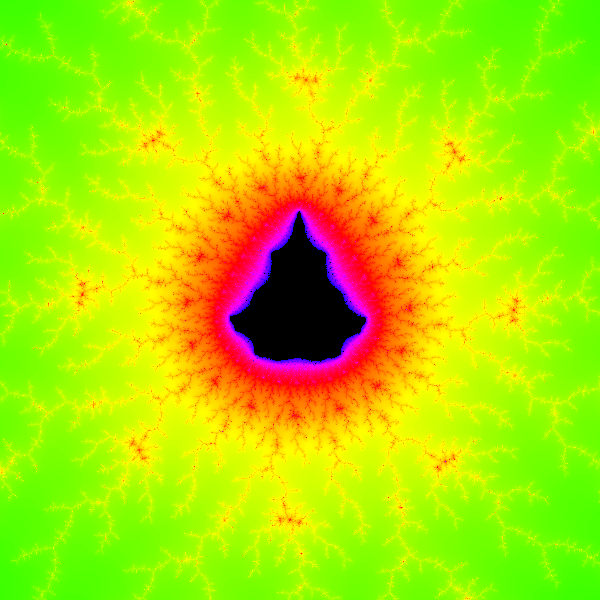
The Mandelbrot set is a complex mathematical object first visualized by mathematician Benoit Mandelbrot in 1980. The set is enormously complex — it is said by some to be the most complex known mathematical entity.
The Mandelbrot set is an example of a kind of mathematics that was always possible in principle, but that only exists in a practical sense because of the advent of cheap computer power. In modern mathematics, computers have changed everything but the basics. Relatively simple conjectures can be verified or falsified in a flash, applied mathematics has been completely transformed, and there is now what can only be called "recreational mathematics" — like the Mandelbrot set, in essence an explorable mathematical landscape.
Algorithm
Notwithstanding its complexity, generating and rendering the Mandelbrot set is relatively easy:
- Establish a two-dimensional complex plane, extending from about -2.0 to +1.0 on the real axis and about -1.5 to +1.5 on the imaginary axis.
- At each point within the plane (using steps determined by the intended graphic resolution), perform this iteration:
(1) $Z \rightarrow Z^2 + C$Where Z is a complex value initially set to zero, and C is a complex coordinate:
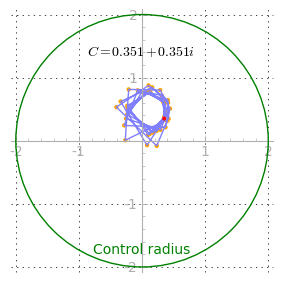
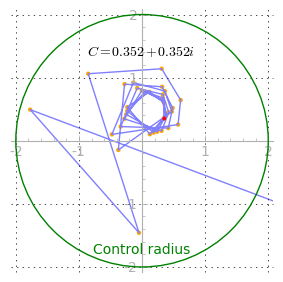
(2) $C = x + yi$where $x,y$ represents a Cartesian two-dimensional coordinate in Mandelbrot space.- For each desired $x,y$ coordinate, repeat the iteration shown in (1) until the $Z$ value either departs toward infinity (in which case that coordinate is not part of the Mandelbrot set), or it orbits perpetually without diverging (in which case it is), as shown in Figures 2 and 3.
In the simplest Mandelbrot generators, each coordinate in the space is tested for membership in the set based on the iteration shown in (1) not diverging toward infinity. Those coordinates belonging to the set are given a distinctive color and the canonical Mandelbrot set shape appears (background of this paragraph). The more elaborate Mandelbrot set generators (like the one on this page) assign different colors to the points on the periphery of the set, based on how quickly they diverge toward infinity.
Execution speed versus image quality
Generators that assign colors use the count of iterations before divergence toward infinity as an index into a table of colors, then assemble a graphic image composed of the colors.
Generator design is a classic computer science problem. At one extreme, a generator can be made very fast by allowing only a few iterations (and colors). At the other extreme, a very high-quality image results from a design that allows many iterations, each of which has an associated color, but at the expense of running time.
The simplest Mandelbrot generators are very simple indeed. Here's a minimal Python example:
#!/usr/bin/env python # -*- coding: utf-8 -*- # Copyright (c) 2013, P. Lutus http://arachnoid.com # Released under the GPL http://www.gnu.org/licenses/gpl.html from numpy import arange # dimensional parameters for the set yl = -1.2 yh = 1.2 ys = .05 xl = -2.05 xh = 0.55 xs = 0.03 def mandelbrot(c): z = 0 for n in range(10): z = z*z + c if(abs(z) > 2): return '.' return '*' s = '' for y in arange(yl,yh,ys): for x in arange(xl,xh,xs): s += mandelbrot(complex(x,y)) s += '\n' print(s)Here is the program's plain-text output with the default settings:
....................................................................................... ....................................................................................... ..............................................................**....................... ...............................................................*....................... ................................................................*..**.................. ................................................................***.................... ...............................................................****.................... ...........................................................***********................. ............................................................**********................. ...........................................................***********................. ...................................................*.......***********..........*...... .................................................****..********************.....*...... ................................................***********************************.... .................................................********************************...... ...............................................**********************************...... .............................................************************************...... .............................................*************************************..... ..........................**......*.........*****************************************.. ............................***********.....***************************************.... ............................********************************************************... ..........................*********************************************************.... .....................*....*********************************************************.... ......................************************************************************..... .....................***********************************************************....... ..*****************************************************************************........ .....................***********************************************************....... ......................************************************************************..... .....................*....*********************************************************.... ..........................*********************************************************.... ............................********************************************************... ............................***********.....***************************************.... ..........................**......*.........*****************************************.. .............................................*************************************..... .............................................************************************...... ...............................................**********************************...... .................................................********************************...... ................................................***********************************.... .................................................****..********************.....*...... ...................................................*.......***********..........*...... ...........................................................***********................. ............................................................**********................. ...........................................................***********................. ...............................................................****.................... ................................................................***.................... ................................................................*..**.................. ...............................................................*....................... ..............................................................**....................... ....................................................................................... Figure 4: Too few iterations/colors
Figure 4: Too few iterations/colors
resulting in bands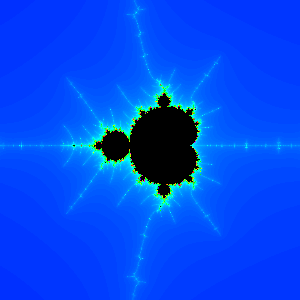 Figure 5: Sufficient iterations/colors
Figure 5: Sufficient iterations/colorsThe most complex Mandelbrot generators accommodate any number of iterations/colors, permit the user to move around within the set and magnify selected areas, and show sometimes beautiful images. Such a generator is built into this page.
Browser Issues
Because the generator runs under JavaScript, I caution my readers that they need to install a modern browser — a list topped by Google Chrome and Mozilla Firefox. For various technical reasons, most other browsers won't be able to run the generator satisfactorily, and most versions of Microsoft's browser won't be able to run it at all (more technical detail appears below the applet).
Color Banding
There is an aesthetic consideration in Mandelbrot set generation: if the generator is configured to allow too few iterations/colors, it will run fast but its images won't be very attractive. When too few iterations are allowed, the transition from one color to another shows up as a series of rather homely bands (Figure 2). The remedy is to increase the number of iterations/colors and accept slower rendering (Figure 3).
Fractal
The Mandelbrot set has the fractal property of self-similarity. As one explores the set, one encounters familiar shapes at increasing magnifications, and examples where a large structure is composed of much smaller components that resemble the large structure. Then it turns out that those smaller structures are composed of yet smaller structures of the same shape. It's initially shocking to increase the magnification from the default of 0.4 to several billion and discover the same kinds of shapes at all magnifications.
Chaos Theory
The Mandelbrot set also has properties of a chaotic system, a system that, even though it appears random in its behavior, is actually a deterministic system that is extraordinarily sensitive to initial conditions. Figure 3 shows how a complex orbit sometimes takes coordinates that seem unpredictable before shooting off toward infinity. The point is that the Mandelbrot set, although very complex, is entirely deterministic — it always produces the same results for given inputs.
Instructions
- After extensive testing, I have reluctantly concluded that no existing Microsoft browsers can run this program. Google Chrome and Mozilla Firefox browsers both run it fine.
- To select a location for further exploration (x,y), click it with your mouse cursor — this will center the desired location.
- To increase/decrease magnification (m), spin your mouse wheel.
- If you don't have a mouse wheel, use the , buttons to change magnification.
- To speed up rendering, choose a smaller image size and/or fewer iterations/colors.
- To increase image quality and to bring out more detail at high magnifications, increase the number of iterations/colors. This requires more rendering time.
To return to the default location and magnification settings, click the button.- To save an image, first choose a suitable image size, then click the button. The rendering engine will create a graphic of the display and place it in a new browser tab. To save the image, right-click the image and choose "Save as ..." or "Save Image as ..." depending on your browser.
- A more complete description with technical details appears below the applet.
| Iterations/Colors: | |
Image size: | | More data
Language Issues
This JavaScript-based Mandelbrot generator is only possible because of vast improvements in JavaScript over the past few years. My first awareness of the change in JavaScript, from a very limited, interpreted (i.e. not compiled), browser-based scripting language, to a more powerful form, was when I tried using it to factor integers as part of an article about prime numbers. To my surprise, as months went by and the JavaScript maintainers continued to improve the language, my prime factoring algorithm ran faster and faster, finally rivaling results from normal compiled languages.
Another improvement made recently, not yet supported by all browsers, is the Worker feature, which allows a JavaScript program to divide a workload among several independent threads, just like a normal compiled language. This generator exploits the Worker feature where it exists to make Mandelbrot rendering blazingly fast — as high as 30 complete renderings per second, for a 600x600 image. The reason for the speed improvement is that many modern computers have multiple processors, and the Worker feature assigns different tasks to different processors.
At the time of writing, the described high performance is limited to two browsers, browsers that represent the cutting edge of browser technology — Google Chrome and Firefox. To see this generator as it should be seen, download one of these browsers:
As time passes, Microsoft's browser falls farther and farther behind the state of the art, and (I am sorry to say) there is no Microsoft browser that can show this generator off to its full potential — or at all.
 Figure 6: HSV-mapped color spectrum
Figure 6: HSV-mapped color spectrumColor Management
In earlier graphics projects I have used a set of key colors and interpolated between them to cover a desired numerical range. But in this project, after much unsatisfactory experimentation, I decided to use an HSV to RGB function to create a pleasing spectrum that maps to the iteration values. When the user changes the iteration/color selection, a new color array is generated that maps HSV values to the numerical range — starting with blue, moving around the spectrum of colors, and back to blue again for the highest values as shown in Figure 6.
One reason this method works so well is because, to show the details of the Mandelbrot set, one must have highly contrasting colors across the entire iteration range. My earlier approaches using key colors inevitably left some areas of the range with changes in hue that weren't sufficient to bring out the details.
 Figure 7: Generator
Figure 7: Generator
thread assignmentMultiprocessing
Before trying to exploit the Worker feature, I did some online research and browsed a number of code examples. After some experimentation and comparison testing, I decided to split the workload among eight worker threads that represent horizontal rectangles in the final image (Figure 7).
When used with a multi-core computer, this threading strategy greatly improves the performance of the generator for a number of non-obvious reasons. Apart from exploiting multiple processors able to function independently, another advantage is that the user may change magnifications or locations while a render is underway. Using conventional coding, a render would complete, then start over with the next change in magnification, however small. Using worker threads, because the user interface is active and on a separate thread, it accumulates any changes without rendering them. Then, when the renderer becomes idle, a single render is made that represents all recent changes.
Worker management
At the time of writing, for security reasons and by default, each worker thread receives full copies of any resources it needs — that's copies, not references. Because the worker renders graphics, it must receive a copy of a large graphics buffer, and when the render is complete, the worker thread must copy the buffer back. This represents a needless processing burden.
As it turns out, there's a method called Transferable Objects in Chrome and Firefox that reduces the severity of this problem. It works by passing references rather than copies back and forth between workers and the primary script, and I have revised the original generator code to take advantage of this feature on those browsers that support it, with a small but significant improvement in rendering speed.
| Home | | Mathematics | |  |  |  Share This Page Share This Page |