 Share This Page
Share This Page| Home | | Science | | * Answers | |  Share This Page Share This Page |
Answers to common questions from social news forums
— P. Lutus — Message Page —
Copyright © 2010, P. Lutus
(double-click any word to see its definition)
Introduction
This page's purpose is to provide carefully written, concise answers to questions frequently seen in online discussions. If these answers don't work for you or leave something important out, or if you have a question you think is a common one with no answer, please let me know.
Evolution: Goal
If evolution's goal is greater intelligence and complexity, why are there still inferior organisms like bacteria?
The answer is that evolution doesn't have goals or preferred outcomes, and evolution proceeds by chance, not design. The primary source of genetic diversity is random changes in genes. These random changes produce changed organisms, but the majority of the changes don't contribute to fitness. Only a small minority help an organism survive and produce offspring, but that is a coincidence and there is no design or intent. As Richard Dawkins puts it, nature is a blind watchmaker.Evolution can produce complex creatures in a relatively short time, not because of a handful of excellent choices, but because of very many perfectly random choices, only a few of which turn out to be choices suitable to their environments. The suitable ones survive and produce offspring. Imagine a primitive Earth, covered with warm salt water, heated by the sun, mixing materials together in random ways, for billions of years. When a biologist studies this history, he begins to wonder how the first primitive life forms could have avoided coming into being.
It's important to understand that the smallest, most "primitive" organisms are the most successful in the random process of evolution. It's likely that bacteria represent 100 times the biomass of all other species combined. Human beings are not the most successful species, and we are certainly not what evolution had in mind, because evolution is not a plan. Read more here.
Cosmology: Big Bang
Where did the Big Bang take place? Can we locate that place? Where is the middle of the universe? What is outside the universe?
Figure 1: "Flatland," a two-dimensional
universe on the surface of a sphere
Click for 3D
The Big Bang didn't happen somewhere in space, the Big Bang is space — the Big Bang created space and time. Because it is difficult to think about these things in three or four dimensions, I ask my readers to think about the universe as though it is the two-dimensional surface of a sphere. Let's pretend the surface is occupied by two-dimensional creatures called "flatlanders" (see Figure 1 on this page).
The flatlanders don't know they're living on the surface of a three-dimensional sphere — their perceptions are limited to two dimensions. They can move around in their world, take measurements, and use geometry (or maybe "flatometry") to draw conclusions.
Remember that flatland is meant to be a simple version of our universe, so flatland had a Big Bang too. At the moment of the flatland Big Bang, the sphere in Figure 1 had a radius of zero — it was a dimensionless point. The Big Bang caused the sphere's radius to increase from zero to its present size. While thinking about that process, try to answer these questions:
- Which part of the sphere's surface is the location of the Big Bang?
- Where is the middle of the sphere's surface?
- Where is the edge of the sphere's surface?
- What is outside the surface?
Because flatland is limited to the sphere's surface, one can see that none of these questions is meaningful except the first — the complete surface, the flatlander's entire universe, is the location of the Big Bang.
Our universe is much like flatland, except that ours has three space dimensions instead of two. And just like the flatlanders, if we should set off to find the edge of the universe, we would eventually arrive back where we started.
We shall not cease from exploration
And the end of all our exploring
Will be to arrive where we started
And know the place for the first time.
— T.S. Eliot
The universe is all of space and all of time. Just like flatland, it doesn't have an inside, an outside, a middle or an edge. And because the Big Bang created time as well as space, it's not meaningful to ask what happened "before" the Big Bang. That would be like asking what is north of the North Pole.
Cosmology: Size
How big is the universe?
Although no one knows for sure, there are some well-supported ideas, and the basis for all our ideas about size come from the circumstances of the Big Bang. Many people have objected to the idea of a Big Bang because it seems to violate a physical principle called "Conservation of Energy." Conservation of energy means energy can't be created or destroyed, only changed in form, and because of the famous equation $E = m c^2 $, what applies to energy must also apply to mass. This means The Big Bang might have violated a basic physical law on the largest imaginable scale.
But it turns out that the Big Bang could have created the universe without breaking physical laws. This can only be true if the Big Bang explosion gave all the universe's mass a particular velocity called "escape velocity." It turns out that escape velocity exactly balances two kinds of energy, one positive and one negative, so the resulting energy is precisely zero.
The universe's positive energy is the sum of all existing energy and mass. The negative energy is called gravitational potential energy. There is a simple way to explain why gravitation is counted as negative energy: if you were standing on the moon and you threw a ball really hard so it had escape velocity, the ball would move away forever, gradually slowing down but never returning. Escape velocity is unique because, at each point in the ball's flight, the sum of positive and negative energy is exactly zero. Then, as the ball's distance approaches infinity, both positive and negative energy become zero, and the ball's velocity becomes zero.
Notice two things about the ball-throw experiment. One, by gradually slowing down to zero velocity but not changing direction, the ball shows that it possesses exactly zero net energy (the sum of positive and negative energy). Two, the only reason for this outcome is because the ball was thrown with escape velocity.
When cosmologists realized this, they saw that it answered the most common objection to the Big Bang — that it violated energy conservation. Naturally enough, they wanted to find out if the universe's mass is moving apart at escape velocity — if it is, this would show that the Big Bang is consistent with physical law.
Figure 2: A triangle in "Flatland"
Click for 3D
Cosmologists realized that the overall curvature of the universe would reveal whether the Big Bang explosion gave escape velocity to the universe's mass (the universe's expansion velocity and curvature are connected). It turns out that "curvature" has the same meaning for our universe that it does for "flatland" (see Figure 1), the imaginary two-dimensional universe lying on the surface of a sphere.
In Figure 2, the flatlanders have drawn a triangle to measure the curvature of their universe. Here are the possible outcomes:
- If flatland has positive curvature as it does in Figure 2, the sum of the triangle's angles will be greater than 180°.
- If flatland has negative curvature, the sum of the angles will be less than 180°.
- If flatland has zero curvature, the angles will sum to exactly 180°.
Can you see why a triangle can be used to measure the curvature of the universe? If a triangle is drawn on a curved surface as in Figure 2, the sides of the triangle follow curved paths, so the angles won't add up to 180°.
To see why, imagine starting at the North Pole, then walking down to zero latitude and longitude (in the Gulf of Guinea off the west coast of Africa). Then make a 90° right turn and walk to 90° West longitude (near the Galapagos Islands off the west coast of South America). Then make another 90° right turn and walk back to the North Pole. The total of the angles is, not 180° as it would be on a flat plane, but 270°. The flatlanders could use this result to discover that their universe has positive curvature.
Cosmologists have similar methods for three dimensions. The difference is that in our universe, space is curved by mass and by gravity. For example, the mass of the Earth curves spacetime in its vicinity, and we sense this as gravity. But on the largest scales, space is curved by the velocity at which the universe is expanding:
Figure 3: A straight line and a point
- If the universe's expansion velocity is less than escape velocity, space is positively curved (as shown in Figure 2).
- If the universe's expansion is greater than escape velocity, the overall curvature will be negative, sort of like a saddle.
- If the universe's expansion is exactly equal to escape velocity, there will be no space curvature — space will be geometrically flat.
So far, our measurements indicate that the Big Bang produced exactly escape velocity, therefore the universe has zero overall curvature. And as it happens, a large-scale spacetime curvature of zero tells us the universe's probable size.
So how big is the universe? Imagine that you are a flatlander, living on the sphere surface shown in Figures 1 and 2. Imagine that you measure the angles of the triangle shown in figure 2, and you discover that the angles add up to exactly 180°. What does this mean? How large must the sphere be for its surface to be perfectly flat?
Here is another similar question, also based on the idea of zero curvature. Let's say there is a perfectly straight line, not curved at all. Let's say there is a point perpendicular to the line, located at such a distance that the point is equidistant to every location on the line. How far away does the point need to be for this description to be true?
Many of my readers will have guessed the answer — these results indicate that the universe is infinite in size.
Cosmology: Multiple Universes
I heard that there are multiple universes. Is this true?
It might be true, but there is no scientific evidence for the idea, and no reliable way to acquire evidence. Many ideas are talked about in science, but only some of them are supported by evidence. This is perfectly all right, as long as people don't confuse speculations and hypotheses with scientific theories. Here is the ranking:
- Speculation: an idea that is inconsistent with existing theory and has no supporting evidence.
- Hypothesis: an idea that is consistent with existing theory but has no supporting evidence.
- Theory: an idea that is consistent with other theories and has supporting evidence.
Every important scientific idea has progressed from speculation to theory, so it's not a criticism to say an idea is only speculation — unless people are confused and believe a speculation is a theory. The fact that we regularly hear about multiple universes on television doesn't mean this idea has ascended to the status of theory, it only means that people find the idea intriguing. People also find the idea of Bigfoot intriguing.
To add to the confusion, there is an unrelated idea from quantum theory called the many-worlds interpretation, that is used to resolve a certain theoretical problem, but this is unrelated to the cosmological question of multiple universes.
Cosmology: Dark Matter & Energy
What is dark matter and dark energy? Are they related?
Dark Matter and Dark Energy are two proposals offered to explain some observations that present physical theory cannot explain. Even though they address different issues, they're related in the sense that neither has an explanation in current theory.
During observations of distant rotating galaxies, astronomers noticed that the outer reaches had rotation rates that were faster than could be explained by the visible matter in those regions. It was as if there was extra mass that couldn't be seen. To deepen the mystery, those areas didn't block light from farther away — this meant the unexplained mass wasn't simply ordinary dark mass like dust clouds, it was something that neither created light nor blocked light from elsewhere.
After carefully considering many possibilities including experimental error, cosmologists reluctantly created a category for the missing mass — Dark Matter. Whatever it is, it doesn't fit into present theory at all.
Dark Energy has a different genesis. First a note of explanation — when an astronomer looks out into space, he is also looking backward in time:
Figure 4: Expansion rate comparison
- A "light-year" is a measure of distance, not time. It is the distance light travels in one year at the speed of light.
- If we look at an object that is one light-year away, we're seeing that object as it looked one year ago.
- A powerful astronomical telescope can see many billions of light-years away, therefore it is capable of looking that far into the past as well.
During observations of the universe's overall expansion rate, astronomers noticed that the overall pattern didn't follow the expected escape velocity profile from Big Bang theory — it seems that the expansion rate is faster now that it should be based on a straightforward application of theory and based on the expansion rate observed billions of years ago.
Again, as with Dark Matter, cosmologists examined many possibilities including experimental error, and reluctantly decided to explain the anomalous expansion by invoking an unexplained universal repulsive force they called Dark Energy.Dark Energy, whatever it is, doesn't work like gravity — it represents a small repulsive force that is unrelated to distance, which means it had no perceptible role in the early universe when both gravitational force and mass-energy density were much higher than they are now.
Even though Dark Energy had little role to play in the universe's past, it will play a much larger role in the future. If present thinking about Dark Energy is confirmed, all the matter in the universe will fly apart in a way that contradicts prevailing theory (see Figure 4).
Neither Dark Matter nor Dark Energy have an explanation, and it turns out that only a small amount of the universe's mass-energy is explained by current theory:
Category Percentage Dark Energy 72.4% Dark Matter 23.0% Conventional Mass-Energy 4.6%
Physics: Speed of Light
Why can't we go faster than the speed of light?
There is an excellent reason, but it will take a few words. Velocity is defined as a rate of change in distance, divided by a rate of change in time, or:
(1) $ \displaystyle v = \frac{dx}{dt}$Where:
- dx = Rate of change in position
- dt = Rate of change in time
If we move ten meters in one second, we have a velocity of ten meters per second. All space velocities are defined with respect to time. And for centuries, time was thought to be a constant, unchanging quantity, the same everywhere, and separate from space.
But in the early part of the 20th century, Albert Einstein and others discovered something interesting about time. It turns out that time is a dimension much like the three space dimensions. In space, you can choose any speed you want. You can go slow — walk on a beach and watch the sun go down. You can go fast — fly in a jet plane. But because time is a dimension, we sometimes travel at different time speeds.
Spacetime
If we come to a stop in space, sit down in a chair, we continue racing through time at time's natural speed, the speed physicists refer to as c, the "speed of light". The difference between space and time is that our speed through time depends on our speed through space. If we have no space speed, our time speed is the same as the speed of light. But as we increase our space speed, our time speed must decrease, according to this relationship:
(2) $ \displaystyle t^2 = c^2 - v^2$Where:
- t = The "speed" of time
- c = The constant speed of light
- v = Our speed in space
So it seems we are racing into the future at the speed of light, mostly along the time dimension. When first confronted by the idea of spacetime, even when space and time appear together in the same equation, many people continue to think of space and time as separate things. But equation (2) shows that space and time are bound together, inseparable. Or, as Einstein's math teacher Hermann Minkowski put it:
"Henceforth, space by itself, and time by itself, are doomed to fade away into mere shadows, and only a kind of union of the two will preserve an independent reality."To show this, let's imagine going faster in the space dimensions. But first, to help understand the process, let's write a normalized spacetime equation, a more flexible form of equation (2):
(3) $ \displaystyle t' = \frac{t}{\sqrt{1-v^2/c^2}}$Where:
- t' = The "speed of time" for space velocity v
- t = The "speed of time" at rest
- v = Space velocity
- c = The speed of light
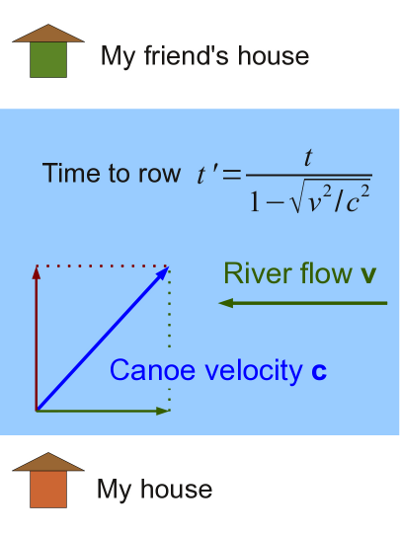 Figure 5: Rowing across a river
Figure 5: Rowing across a riverEquation (3) is the simplest expression showing the relationship between space and time — it shows that time is a dimension, much like the space dimensions, but it is treated differently — space intervals are subtracted from time intervals.
This is the single most important thing to understand about the relationship between space and time: space speed comes at the expense of time "speed" — if we go faster in space, we must go slower in time.
The River
Here's an everyday example that may help explain it. Let's say I live next to a river and I can only row my canoe at a fixed speed of c (c = canoe). But the river's flow velocity changes during the year — let's call the river flow velocity v. I regularly row across the river to visit my friends, and I want to know how long it will take me to get across the river when the river's velocity is v. We'll be using equation (3) above, but we'll give the variables different meanings:
- t' = Time to row across the river with flow rate v
- t = Time to row across a calm river
- v = The river's flow rate
- c = My fixed canoe rowing speed
Let's say it takes me 15 minutes to row across the river when the water is calm. But the river has different flow rates at different times of the year, and it sometimes flows as fast as I can row. If the river's velocity is 99% of my rowing speed, my rowing time will be:
(4) $ \displaystyle t' = \frac{15}{\sqrt{1-(99/100)^2}}$
River flow velocity v
in terms of c (v/c)Canoe rowing time
years, days, h:m:s1-1x10-00 (0) 0000 y 000 d 00:15:00 1-1x10-02 (0.99) 0000 y 000 d 01:46:19 1-1x10-04 (0.9999) 0000 y 000 d 17:40:41 1-1x10-06 0000 y 007 d 08:46:36 1-1x10-08 0000 y 073 d 15:46:01 1-1x10-10 0002 y 006 d 13:40:07 1-1x10-12 0020 y 065 d 18:39:02 1-1x10-14 0201 y 321 d 09:50:42 1-1x10-16 1915 y 075 d 16:00:00 1.0 With a result of 1 hour, 46 minutes, and 19 seconds. Figure 6 shows more results for rowing across the river:
- The left column is the river velocity in terms of my canoe rowing speed c, or v/c.
- The right column is the rowing time for that river velocity.
- As the river velocity in the left column becomes closer to my rowing speed, my rowing time becomes longer.
- And if the river should flow as fast as I can row, my rowing time would become infinite — I wouldn't get across the river no matter how much I rowed. It would be as though time had stopped.
Refer again to Figure 5, the river diagram:
- If the river is calm, I can row directly across to my friend's house with minimum time and effort.
- When the river is flowing to the left, to get to my friend's house most efficiently, I have to turn my canoe to the right and paddle diagonally.
- As the river's flow increases, I have to turn my canoe farther to the right.
- Finally, when the river's flow equals my rowing speed, I have to turn 90° and row straight along the river, which means I cannot cross, no matter how much time passes. The required rowing time has become infinite.
Now refer to Figure 7, an interactive speed-of-light applet, in which a right triangle represents the relationship between space and time:Figure 7: Interactive Speed-of-Light Applet
- The vertical axis, labeled "t", stands for the time dimension. In the canoe example, it was the canoe's motion across the river, toward the opposite bank.
- The triangle's hypotenuse, labeled "c", stands for the speed of light. In the canoe example, it was my constant rowing speed. That seems appropriate because the speed of light is also constant and unchanging.
- The horizontal axis, labeled "s", stands for the space dimensions. In the canoe example, it was the canoe's motion along the river, toward the right.
Play with the speed-of-light applet. Drag your pointing device from side to side on the applet and see how it changes the relationship between space and time. Notice that time can only pass at full speed when there is no space speed, and when space speed equals the speed of light, time stops.
The meaning of this exposition is that c, the speed of light, defines the relationship between the space and time dimensions:
(5) $ \displaystyle c^2 = t^2 + v^2 $Where:
- c = The constant speed of light
- t = The "speed" of time
- v = Space velocity
Equation (5), a restatement of equation (2), shows that c is the fundamental unit, not time and not space. If space speed increases, this doesn't change c, instead it changes time. This is the real meaning of the often-heard remark that the speed of light is constant in all frames of reference. This is so because the speed of light is more fundamental to nature than either time or space.
Mass
Let's say you are in a spaceship moving at high speed. The equations on this page show that time must slow down when space speed goes up, but can the spaceship's passengers sense this? Well, no, because everything on the ship is slowed down — the clocks, the machines, even the people. Because biology slows down along with everything else, there is no way for people or instruments to detect a local change in the rate at which time passes.
But an observer on a different ship (let's say ship B) traveling at a different speed (or no speed) would be able to see the time difference on ship A. Let's say the people on high-speed ship A want to measure a mass. In space there are no consistent, fixed gravitational forces, so simply weighing a mass is out. But there is a reliable way to measure mass anywhere — just push the mass with a spring and time the rate at which the mass acquires velocity.
The people on spaceship A run the mass test, and the results are exactly the same as they would be without any speed. But the people on spaceship B watch the test being conducted on A, and because of A's time dilation (seen by B but not A), they say the mass is greater.
So, to the observers on ship B, A's mass test result is different — the mass is greater. Is this because the mass on ship A is really greater, or is it because A's time is passing at a different rate? It turns out this is not a meaningful question — both descriptions are true and interchangeable. To see why, imagine that ship A tries to accelerate using its rocket engines. The observers on B notice that A's rocket engines seem to be performing correctly, but they can't accelerate the ship at the usual rate. This is for the same reason that the spring couldn't push the mass at the usual rate.
So as a spaceship acquires velocity, its time rate goes down (experiment with the speed-of-light applet), which means the spacecraft gains mass, which means the rocket engines would have to deliver more power to change the ship's velocity in a given amount of time. Because time dilation and mass increase both approach infinity, the ship cannot get to the speed of light.
The canoe example is helpful in this connection:
- As the river's speed approaches my fixed paddling speed, I'm no longer able to add any more velocity. I put out massive amounts of energy, but I am stuck in space.
- As a spacecraft's speed approaches the fixed speed of light, it's no longer able to add any more velocity. It puts out massive amounts of energy, but it is stuck in time.
Science: Correlation vs. Causation
I read a science article that claims people who take a daily vitamin end up smarter than those who don't. Is this important?
It might be important, but in many cases, such a study is neither important nor science. Many studies get a lot of undeserved press coverage because:
- To hold onto its readers, the popular science press needs a steady stream of "breakthroughs," even when there aren't any to be had.
- Scientists need to publish articles to advance their careers, and the number of articles is more important than their quality.
- People prefer "science" articles that include dramatic conclusions and results, even if this contradicts the facts.
People who aren't trained in science tend to read such articles and think that a correlation between two things — call them A and B — means that A caused B or the reverse. But, as is often said, correlation does not imply causation. This means people not trained in science tend to see a cause-effect relationship where none exists, in circumstances where a more disciplined observer might ask some hard questions.
Bad Science
It might surprise my readers to know that the majority of "discoveries" reported in the popular science press turn out to be either falsified later, or are abandoned without any effort to repeat the original work (replication of results is essential to real science). Here is an example of science at its worst:
- A scientist has an idea he thinks is true.
- To test his idea, he signs up members of the general population that have behaviors relevant to his idea, for example they might take a daily vitamin.
- After the scientist has some data that shows a correlation between two traits A and B, the scientist rushes to publish the "result," the "finding." He does this because publication is essential to a scientist's academic survival.
- Many such studies are published without any effort to either suggest or test a cause-effect relationship.
- The article body invariably includes qualifiers (it's just a preliminary finding, more work is needed, we don't know the reason for this correlation, etc.), but in the popular science press, the headline often flatly contradicts the article itself.
Here's an example I picked at random on the day I wrote this piece. I could find several fresh examples any day of the year, but this one happened to catch my eye:
- The link: Sunlight may save kids’ sight
- The article subtitle: "Australian researchers have found exposure to sunlight could be a critical factor in stopping children from becoming short-sighted."
- Needless to say, the article contains no evidence whatsoever to show a cause-effect link between lack of exposure to sunlight and nearsightedness, and no established theory that supports this idea.
- The authors of the article go out of their way to flatly contradict the implication of the headline: "He [the author of the study] says while they will begin experiments to assess this theory, the findings are concrete enough to inform public health policy."
- Translated into plain language, the authors found an unexplained correlation, have only an untested theory about it, but are perfectly happy to imply a cause-effect relationship that isn't supported either by established theory or evidence, and they're more than willing to raise a public alarm as though they have a scientific result.
A more likely explanation is obvious — kids who spend a lot of time playing outside are less likely to bias their young, flexible eyes into nearsightedness by staring at the nearby pages of a book, or TV set, or computer monitor. But this explanation, the conventional one, won't get you published in a science journal, and won't win you a professorship or tenure.
Good Science
For contrast, here is how real science works:
- A scientist might observe something in nature and decide to study it, but without any preconceived idea about what it might mean.
- After gathering data, the scientist might propose an explanation, preferably one that agrees with established theory.
- Consistent with high scientific standards, the scientist would then propose a test of the explanation that will either support or falsify his idea — that will either show, or disprove, a cause-effect relationship between A and B.
- If the test is successful, other laboratories will try to replicate the study based on the original author's description.
- If the study is successfully replicated, the idea and experimental results might be suitable to publish in the general science press, and to shape public policy.
Unfortunately, this recipe is almost never followed.
Falsifiability
A bedrock principle of science, a requirement for any theory that merits the name "scientific", is that it be falsifiable in a practical test. This doesn't mean that every theory is false, it means a theory needs to be open to falsification — the theory's claims must be testable and, if the tests fail, the theory must be discarded.
In order for the falsifiability requirement to be met, there must be a proposed explanation that links cause A and effect B. If we only have a description, for example "smart people take vitamins," there is no basis for falsification — it's just a description.
As it turns out, because of the competitive and commercial nature of modern science, most of the "scientific" ideas the public hears aren't science at all, and pubic policy is often shaped by unsupported conjectures that will never rise to the level of science.
There was a time when scientists were willing to be as skeptical as true science requires, to ask the tough questions that lead to real science. Instead, we see publication of hundreds of results that don't merit the name "science." For example, about the question that led to this article, is it true that vitamins make people smarter? Let's see:
- We'll poll the public and ask two questions:
- "How smart are you?" and
- "Do you take a vitamin?"
- If the smart people take more vitamins than the dumb people, then it's proven and we'll publish our scientific result.
To someone trained in science, this is a ridiculous study — it fails to account for the possibility that smart people are more likely to take a vitamin because of their greater knowledge of health issues. In other words, cause and effect might be reversed.
Most Studies are False
Here is a research finding the public won't be likely to read in the popular science press — most published scientific findings are false. Some of the reasons for this are provided above — ambitious scientists, a gullible, uneducated public — but the fact that this is itself a scientific finding may come as a surprise.
In one of the articles revealing this fact — "Why Most Published Research Findings Are False" — the authors describe some of the factors I show above:
- Marginal findings in small fields tend to seem more statistically significant than they really are.
- There is a tendency toward "data mining" — searching for anything suggesting statistical significance and publishing it without considering that it might result from chance rather than correlation.
- Many researchers begin a study with a preconceived idea about the outcome, and may ignore contradicting evidence. This is called "confirmation bias."
- There is often a financial incentive to publish dubious results in advance of competitors, solely to establish priority over something that may not be true at all.
- High publication rates assure personal academic advancement.
Most of these problems would be alleviated by public education in the principles of science. Science would be greatly served by an educated public, a pubic willing to say, "Where's the evidence?"
Further reading on this topic: The Doubt Factory
What is a Crackpot?
I hear the expression "crackpot" and I think it's not defined very well. Do you have a definition?
Some people think a crackpot might be an Einstein who hasn't been discovered yet. Others think crackpots are people who insist they are an Einstein who hasn't been discovered yet, but without any connection to reality. The truth is somewhere between.
A classic crackpot is an Internet forum participant who constantly talks about his pet idea, who tries to turn every discussion into a debate about his idea, and who seems oblivious to contradicting evidence. Another distinguishing crackpot trait is that he doesn't think it's his responsibility to defend the idea, but the responsibility of others to disprove it.
To begin, we need to define what the word "theory" means in science, and how it differs from speculations and hpotheses:
- Speculation: an idea that is not consistent with established theories and has no supporting evidence.
- Hypothesis: an idea that is consistent with established theories but has no supporting evidence.
- Theory: an idea that is consistent with other theories, has supporting evidence, and is falsifiable in practical tests.
The falsifiability criterion is very important in science — every scientific theory must be testable and falsifiable in practical tests, or it cannnot be accepted as scientific. The most important difference between astrology and astronomy is that astronomy is falsifiable and resists efforts at falsification.
A scientist who has an idea understands his responsibility to produce evidence for the idea, evidence collected in scientific experiments, evidence that distinguishes his idea from other ideas. A scientist will offer a basis for falsifying his idea — a test that, if it fails, would invalidate his idea and cause it to be abandoned. A scientist assumes his idea is false unless and until there is supporting evidence (this is called the null hypothesis).
A crackpot doesn't think it is his responsibility to defend his idea, instead he believes it is the responsibility of others to falsify it, and unless someone else falsifies it, he thinks his idea must be true — the opposite of the scientific perspective.
A scientist will say, "I have an idea, but I haven't located evidence that distinguishes it from other ideas, so my idea is just a hypothesis and my job has just begun." He then will accept personal responsiblity for locating evidence, and he will remain open to the possibility of contradicting evidence.
A crackpot will say, "I have an idea, but others haven't succeeded in disproving it, so it must be true, and my job is done." He then will argue in favor of his idea, will selectively pick and choose only arguments that support it, and he will refuse to consider contradicting evidence (this is called "confirmation bias").
The crackpot's perspective contains several fatal logical flaws, the most important of which is his attitude toward evidence. As explained above the crackpot will say, "Unless my critics can disprove my idea, it must be true."
Let's consider a specific example. Let's say the crackpot believes in Bigfoot. He says, "Unless my critics can prove that Bigfoot doesn't exist, then Bigfoot exists and I am right." The problems:
- This posture shifts the burden of evidence away from the crackpot (where it belongs) to his critics. Science requires that the originator of an idea accept responsibility for supporting his idea.
- This posture requires proof of a negative, in many cases an impossible evidentiary burden. For example, it's not possible to prove that Bigfoot doesn't exist, it would only be possible to prove that he does by locating an example.
- Requiring proof of a negative means the crackpot can continue to believe in things for which there is no evidence whatsoever — Bigfoot, alien abductions, religious miracles, Men in Black, the second gunman on the grassy knoll, you name it. Requiring proof of a negative is a powerful tool in support of ignorance and superstition.
The crackpot bottom line is that there are scientific and evidentiary requirements that crackpots invariably refuse to accept:
- The burden of evidence for a claim rests with the claimant, no one else.
- "Extraordinary claims require extraordinary evidence." — Carl Sagan
- A crackpot's idea must be accompanied not just by evidence, but evidence that distinguishes it from existing theories. Otherwise any idea is validated through similarity with accepted ideas.
- Proof must be positive, not negative. The fact that something has not been disproven doesn't represent evidence in its favor.
- Any legitimate scientific idea must be open to falsification using evidence.
Here is how crackpottery works in real life — let's say I am a crackpot and I have invented a miracle cure for the common cold. My magic cure is to shake a dried gourd over the cold victim until he is all better. If I shake the dried gourd long enough, the victim's cold will get better. My miracle cure always works, it is 100% effective, it is extremely reliable. I deserve recognition for my medical breakthrough. Anyone who wants to dispute my claim must prove that it doesn't work — that all those people who got better, didn't get better.
The crackpot's logic is perfect, and perfectly loony.
Crackpots come in many varieties, but they all have one trait in common — they don't understand how science works.
Read this article for more depth on this topic.
| Home | | Science | | * Answers | |  Share This Page Share This Page |