
 Share This Page
Share This Page| Home | | Orbital Modeling | |  |  Share This Page Share This Page |
Section 3. JWST Lagrange Orbit Analysis
— P. Lutus — Message Page —
Copyright © 2022, P. Lutus
Most recent update:
In this section I present the results of my analysis of the JWST orbit around the Lagrange L2 point. Lagrange points have been known to exist for some time and their properties well-established in theory. Some space missions have used them for low-energy station-keeping, but to my knowledge no earlier projects have attempted to orbit one.
The reason for the orbit around Lagrange point L2 is that if instead we located JWST at the exact L2 point (see graphic above and interactive space application below), this would place the spacecraft directly in line with the earth and sun. In this alignment, solar radio-frequency interference would overwhelm the Earth uplink transmitter signal and prevent the craft from detecting essential communications.
The chosen remedy is to make the JWST enter a semi-stable orbit around the Lagrange L2 point in such a way that it's never directly in line with the sun-earth axis.
Before describing this orbit in depth, and on the theory that a picture is worth a thousand words, here's an interactive Lagrange orbit simulator:
- Click the "Animate" check-box to start a live animation of the orbit.
- Click the "Anaglyphic" check-box to enable a 3D view available using red/cyan (
) glasses.
- Drag your mouse/pointer to rotate image in X/Y dimensions.
- Ctrl+drag to pan image in X and Y dimensions.
- Mouse wheel zooms the image.
- Press space bar to pause the animation.
- Tablet gestures are supported:
- One finger: rotate.
- Two fingers: pan and zoom.
James Webb Space Telescope Lagrange Point L2 Orbit (click here) for a larger 3D viewer
Animate Anaglyphic 3D () Reference Grid Translate to L2 Include Moon's Gravity
Note: This application doesn't generate orbital data in real-time. Instead, to keep from burdening your browser, it relies on a data archive created by a Rust-powered orbital data generator — see this article's Section 2 for the details.
At the time of writing, the James Webb Space Telescope is in a rather peculiarly shaped orbit around Earth's Lagrange L2 point, out past Earth's orbit by the so-called Hill Sphere radius of roughly $1.5 \times 10^9$ meters. In the above application this point ls labeled "L2".
Lagrange points are, in the case of the earth, five orbital points of relative stability (see the title image at the top of this page) where a spacecraft or an asteroid may dwell for an extended period with little or no fuel expenditure required to maintain its position. This orbital stability makes Lagrange points especially important for space missions that need to remain synchronized with respect to earth's orbit:
Lagrange Point Location and Radius L1 On the axis line joining Earth and sun, located at the inner boundary of Earth's Hill Sphere radius. L2 On the axis line joining Earth and sun, located at the outer boundary of Earth's Hill Sphere radius. L3 On the axis line joining Earth and sun, but on the opposite side of the sun at Earth's orbital radius. L4 60° "behind" Earth (counterclockwise in this page's title image), along Earth's orbital path at the same radial distance from the sun. L5 60° "ahead" of Earth, (clockwise in this page's title image), along Earth's orbital path at the same radial distance from the sun. It's important to emphasize that Lagrange points aren't gravity wells and don't maintain a firm hold on their visitors. It's more accurate to say they don't immediately expel objects that are positioned at them. But over time, without a fuel expenditure or other stabilizing force, objects will drift away.
Again, the reason for the JWST's orbit around Lagrange L2 is to allow reliable radio communication with Earth, a goal that requires the spacecraft to avoid the Sun-Earth axis line.
But having said that, the JWST Lagrange L2 orbital shape is quite strange — the plane of the orbit is tilted about 28° away from perpendicular to the ecliptic plane, as clearly seen in the above orbital application. At first this makes one think the orbit is unstable or destined to be short-lived. But the explanation for this tilt is reasonably straightforward:
- The above interactive application subtracts Earth's orbital motion and rotation, a convenience to permit focus on the JWST and its orbit. This may make readers forget that in reality the JWST's orbit is being rotated by the Earth's orbit, and the two orbits are nearly perpendicular to each other.
- This means as the JWST ascends and descends through its orbit, Earth's simultaneous orbital motion twists the JWST's path — away from the Earth when ascending (+Z) and toward the Earth when descending (-Z).
- The strength of this effect depends very much on the JWST's orbital velocity, and I have found stable orbits around the Langrage L2 point that would make the JWST's orbit lie on the same plane as Earth's orbital plane. Of course, such an orbit would defeat its original purpose.
As it turns out, NASA (and the Space Telescope Science Institute (STScI)) anticipated this odd orbit and planned the mission taking it into account. Here is one of the STScI's descriptive JWST graphics (click the image for full-size):
Here's a similar graphic derived from my current orbital model (distances in meters):
Remember about these diagrams that they subtract Earth's orbital motion to be able to focus on the JWST's orbit and related issues. The STScI diagram above says it this way: "Trajectories [are] shown in the Rotating Libration Point (RLP) frame." I think the reason for the orbital tilt would be more obvious if both orbits (that of the Earth as well as the spacecraft) were displayed at once. But that animation would be very hard to interpret.
Earth's moon has a strong effect on the path and overall stability of the JWST orbit. Astute observers will notice some seemingly random wandering in the JWST orbital path shown in the above application and in the orthogonal-dimensions chart as well. This results from gravitational interactions between the Earth, the moon and the spacecraft.
Curious about these effects I ran a test. I disabled the JWST's orbit and positioned it directly at L2 to see how much it wandered from that spot in two years. Here's a space animation showing how much a hypothetical, relatively stationary craft would wander from L2 only under the influence of the Earth's and moon's masses:
Lagrange Point L2 Closeup View
X axis scale is approximately 50,000 km. The dotted line is the Sun-Earth axis.
Animate Anaglyphic 3D () Include Moon's Gravitational Effect
This animation compresses two years of simulator time to 24 seconds (730 days, 730 frames, 30 frames per second). Note the rapid (less than one second) loops in the JWST's position — these result from the moon's direct gravitational effect on JWST (in this time-compressed video the moon requires about one second per orbit). The slower spacecraft motions result from the orbiting Earth's effect on masses at the Lagrange L2 point during two orbits, two years. If Earth's orbit were perfectly circular, not at all eccentric, these slow changes would probably not be present.
This no-orbit dwell-at-L2 test shows what secondary forces are at work on the JWST during its established orbit, and explains most of the observed irregularities in that orbit.
I once thought Lagrange points were gravity wells (meaning self-balancing space locations that sucked objects in), but in experiments with my solar system model I discovered this isn't so. In fact, without station-keeping fuel or another energy source, a craft (or an asteroid) is certain to drift away from a Lagrange point in time. One might say that remaining at a Lagrange point without energy expenditure is like balancing a pencil on its tip.
So given this natural instability, how did I keep my model JWST in orbit around Lagrange L2 for two years (as shown in the space view applications on this page) — why didn't the craft just drift away over time?
Well ... it eventually did. It just took two years for the modeled craft to lose its delicate balance and drift away. In the Lagrange Point L2 Closeup View above, at the two-year time mark, the craft suddenly speeds away.
I acquired two model years of stability with a fine-tuning search strategy that uses a binary search algorithm to locate the perfect initial velocity for the orbiting case or the perfect location near the L2 point for the stationary case. Binary search is a classic computer goal-seeking strategy that, if properly set up, can find optimal values in a sea of competing alternatives.
I used my search algorithm to locate a numeric constant that adjusts my model's behavior and allows the craft to remain in orbit (or on station at L2) for 730 days before beginning to drift away. I discovered this would only work if the numeric value was defined to a precision of ... wait for it ... ten decimal places.
I was astonished — ten decimal places were significant. Anything less precise and the craft would prematurely drift away from a "Goldilocks zone" of temporary stability.
Here are some "Goldilocks Zone" test results — three numerical control values and three model outcomes that arise from them (for each numeric constant I've emphasized the key decimal place and changed value in red):
Lagrange Goldilocks Zone Test
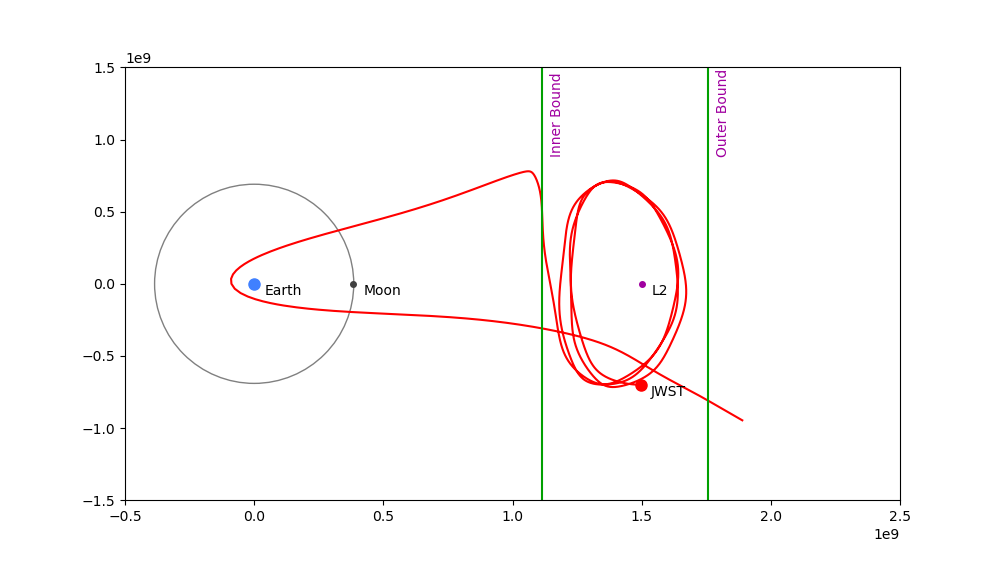
Correction Value Too Small: 0.9930677550252303
Outcome: Craft falls toward Earth and tries to orbit it.
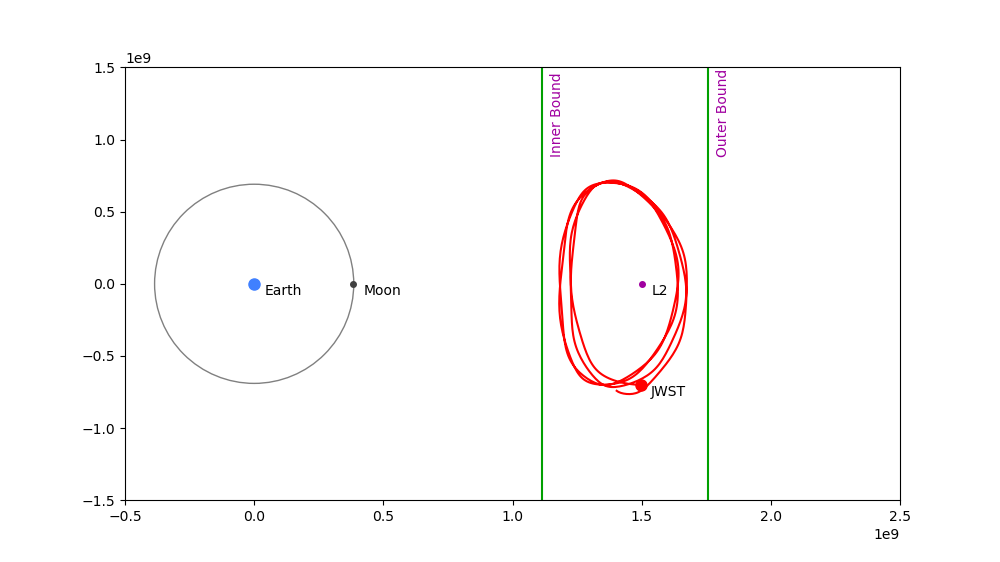
Correction Value Just Right: 0.9930677551252303
Outcome: Craft remains stable for 730 days.
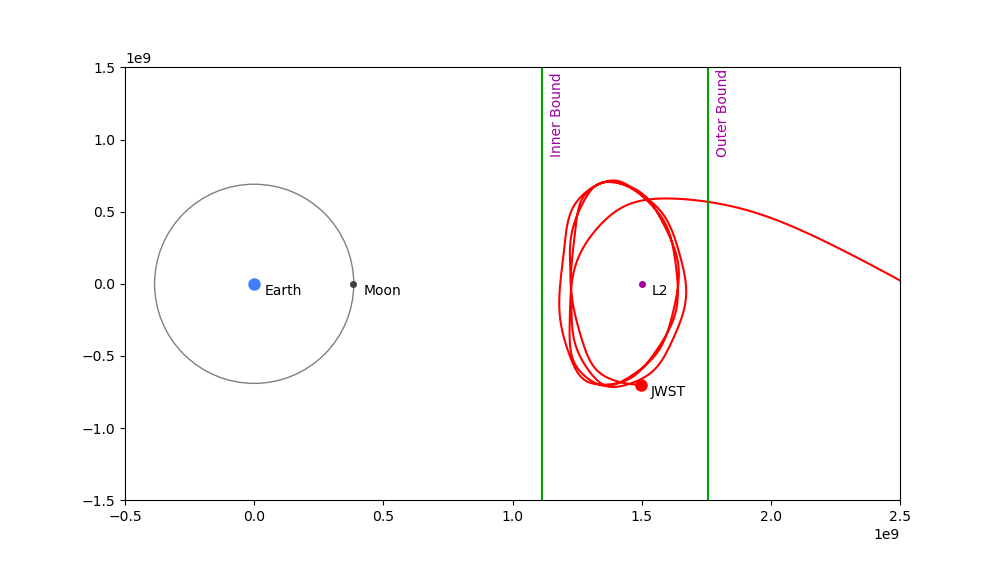
Correction Value Too Large: 0.9930677552252303
Outcome: Craft drifts away from L2 toward Mars.
I acquired these results using the classic binary search strategy. I began with an adjustment value like 0.5 and ran the orbit simulator. If the craft crossed the Inner or Outer Bound shown in the above images, I changed the adjustment value's sign, divided it by two and tried again. A successful search required 50 or 60 full orbital simulations, which explains why Rust's execution speed was essential to the project.
All my test proves is that Lagrange points aren't self-stabilizing, and to dwell at L2, some station-keeping fuel burns are required.
The JWST operators know this and expect to burn fuel periodically to keep the craft on station. In this space.com article, we read, 'Lagrange points are sometimes nicknamed "parking" spots for spacecraft, as they mark locations where the gravitational tugs of different bodies balance out. However, throughout its stay at L2, Webb will need to conduct occasional small thruster burns for "station keeping" and "momentum management" to retain its proper location and orientation in space. That's what the propellant remaining after the third burn will be used for.' Although not emphasized in the article, when that fuel is used up, the mission ends.
Can the JWST operators save fuel by using the strategy I used here? Well, no, not really — several reasons:
My model doesn't include chance factors the real JWST will experience — solar wind flux, photon pressure and other factors — that can't be anticipated or controlled.
The JWST has a special requirement that prevents its operators from trying for a perfect balance of forces as I did in this experiment, and that is: the JWST must always be oriented to thrust away from the sun during its mission lifetime, because if it ever had to turn around to thrust toward the sun to regain its orbit, the entire science facility, normally protected from the sun by an ingenious heat shield, would overheat and need to cool back down again, with a great loss of time and instrument stability.
Therefore to be always faced away from the sun even when adjusting its orbit, the JWST must slowly drift toward Earth and sun. It can't try for a zero-energy, perfectly balanced solution as in this experiment.
To date this has been my most complete and accurate orbital model and it's been very satisfying. I began this project for two reasons — one, I wanted to know whether Lagrange points were gravity wells or hilltops (where spacecraft eventually fall off), and two, I read an article that showed the tilted orbit NASA expected for the JWST and I wanted to know the reason for that orientation.
I got all my questions answered and a few more I didn't initially know to ask, so this has been an educational adventure as well as a rewarding computer programming experience, both on my short list of favorite things.
Thanks for reading!
| Home | | Orbital Modeling | |  |  Share This Page Share This Page |