 Share This Page
Share This Page| Home | | Mathematics | | * Is Mathematics a Science? | |  Share This Page Share This Page |
For some, the question isn't rhetorical.
— P. Lutus — Message Page — Copyright © 2008, P. Lutus Background | Science Defined | Varieties of Mathematics(double-click any word to see its definition)
Background
Update 2015: After much thought, I no longer think math is a science. Science must be empirical, meaning it must be based on observations of nature, and it must be potentially falsifiable by new observations of nature. This article makes some valid points but doesn't adequately emphasize science's empirical requirement. I'm leaving this article on my website as a historical artifact, not as a reflection of my current views.
For a detailed exposition of why, in spite of its great importance to science, math cannot itself be a science, read my more recent article Scientific Paradigm.This article is meant to be a counterpoint to my article "Is Psychology a Science?", an article that has led to a somewhat circular debate about the nature of science, a debate whose fervor increases in inverse proportion to the presence of testable propositions. During that debate I've heard from a number of psychologists and others who, in the heat of the moment, have claimed mathematics isn't a science. Here are two representative quotes:
- "In passing, I'll observe that mathematics is not a science either, contrary to your claim ... Mathematics is a formal logic game, resting on untested (and untestable) principles of representation and meaning (e.g., the notion of symbol), logic and deduction (e.g., syllogism), definition (e.g., set)."
- "Mathematics is a formal abstraction of quantity and logical deduction. There is no concept of evidence within it. Everything is deductive. Deduction is a fundamentally different kind of knowledge than observation. You can do it all in your head, with your eyes shut, in a sensory deprivation tank, at least in principle. There's no such thing as mathematical hypotheses and experiments."
Educated readers will quickly see the errors in these positions, but I regularly hear from people who hold views like these (they are invariably people unfamiliar with mathematics). In this article I address these claims in a way that I hope will prove useful even for those already familiar with the place of mathematics among sciences.
In this article I present mathematical hypotheses, experiments and results, in order to show that these elements of science are present in mathematics, indeed they represent the essence of mathematical reasoning. The primary handicap while discussing science in psychology is that one is placed in the position of trying to demonstrate the absence of something, a tenuous debating position. By contrast, in this article I am able to show the presence in mathematics of all key elements of science, e.g. theory, evidence, and falsifiability.
Science Defined

Before we test the connection between mathematics and science, we should define science. We might otherwise make a plausible claim based on an implausible premise. The essentials of science are:
- Evidence gathered in experiments and observations.
- Theories about the evidence, theories that move from the particular to the general.
- The requirement that contradicting evidence falsify a theory.
I placed these elements in a readable order, but the third element is by far the most important — the so-called "falsifiability criterion" is what sets science apart from superstition. Also, elements (1) and (2) are interchangeable — one might shape a theory before evidence (as in relativity), or gather evidence in advance of a theory (quantum mechanics), but however one arranges (1) and (2), they must lead to (3): falsifiability. This doesn't mean scientific theories are legitimized by being falsified, it means they are perpetually subject to falsification by evidence.
That is the unadorned kernel of science. But people sometimes confuse these core issues with less important points like where and how one gathers evidence. However it is gathered, evidence must be unambiguous and repeatable, and it must be objective (two impartial observers must come to the same conclusion).
As it turns out, science doesn't require that evidence come from nature. If I invent an imaginary world with clearly expressed, consistent rules, I can use the rules to gather meaningful evidence about that imaginary world and I can shape a falsifiable theory based on observation. The result is scientific because the evidence looks the same to all observers, and because the derived theories can be falsified using evidence. Astute readers will see that this is more than a hypothetical argument — some mathematical systems represent just such an imaginary, detailed, internally consistent world amenable to scientific study.
People sometimes create an imaginary world and falsely claim it represents nature, but that is a separate issue. There are various reliable ways to establish whether a mathematical model has a corollary in nature.
Varieties of Mathematics

If we look on mathematics as an imaginary world with no connection to reality, we can still do science. Let's call that "Platonic mathematics." If instead we claim that mathematics is nature's language, then we can explore nature through mathematics, and again, it's legitimate science. Let's call that "natural mathematics."
I propose these definitions:
Platonic mathematics the kind of mathematics having no essential connection with the physical world. I say "essential connection" because links between nature and esoteric mathematical notions spring up in unexpected places, like the surprising connection between locusts and prime numbers. Natural mathematics the kind of mathematics arising from the uncanny efficiency with which mathematics describes nature. In this article we will explore science derived from both Platonic and natural mathematics.
The Platonic Playground
At first glance Platonic mathematics appears to represent a challenge to the conventional understanding of science. In the common view, one tests theories against nature — but nature is just one source of experimental evidence, it's not the only one. Any internally consistent system can serve as a source of theories and experimental evidence.
This argument can be turned on its head — there is a longstanding belief about nature that it will turn out to be based on a handful of easily expressed rules, and the only reason we don't know those rules is because we haven't thought about them hard enough. It turns out that our expectations about nature have a lot in common with our expectations about mathematics — simple, easily expressed theories tend to prevail over complex ones. It is important to understand that this precept (popularly known as "Occam's Razor") is vindicated repeatedly in the history of science — as time passes, more and more of nature is described using fewer, simpler rules.
My point is that we expect to be able to craft a realistic theory about nature that is expressible in a few algorithms or equations, but that can reliably produce something very complex in nature. It is only a small conceptual step from there to the notion of an internally consistent, testable system that is not intended to represent nature, but that can be explored just as though it did.
Now let's express a hypothesis about a system disconnected from nature, then gather evidence from the system. My intent is to show that all essential scientific criteria can be met by a purely mathematical idea.
Euler's Prime Generator Function
Let's say I make the claim that this function —
f(x) = x2 + x + 41 (from Euler)— if provided with natural numbers as arguments, will produce only prime numbers (numbers divisible only by themselves and one) as results.
This claim has all the properties required for science — it poses a theory testable using evidence, and if the evidence contradicts it, the theory is falsified. And it even possesses a diligence factor — if the experiment isn't conducted with sufficient zeal, it may produce an unreliable result.
As it turns out, this remarkable function will generate a prime result for each argument in the range 0 <= x <= 39, but at x = 40 it fails. Back in the days of hand computation, several days might be required to generate and test the results. This problem also has what I call a "coffee break" property — we might start at zero, struggle up to 39 and then ... coffee break!
Euler's prime generator makes a statement about pure mathematics, not nature, yet it is testable and falsifiable in a scientific way.
 Monty Hall
Monty HallThis is a problem that only appears to be connected to nature — it is actually an example of Platonic mathematics. The fact that it involves a game show host (Monty Hall), a contestant and a set of doors hiding a prize is coincidental — the game-show setting is just a convenient way to state a problem from the realm of pure mathematics.
In the game, you've chosen one of three doors, behind which you hope is a nice car, but if you've chosen badly, you get a goat. Monty Hall then teases you by opening one of the two unselected doors and revealing a goat (he always chooses a losing door), and he offers you the option of switching doors. Is there an advantage in changing doors?
At first glance, there doesn't seem to be an advantage in switching — the prize's placement is random and the two unopened doors are equally likely to contain the prize. But counterintuitively, if you do not take Monty Hall's offer, your overall chance of winning is 1/3, but by switching doors your chance to win rises to 2/3 — you double your chances!
This counterintuitive outcome is called a "veridical paradox" — not a classic paradox, but a result that defies intuition.
This problem originally appeared in Parade magazine in a column written by Marilyn Vos Savant, a woman reputed to have a very high I.Q.. After publication about 10,000 readers, including many academics, wrote to object that the published result was wrong. One issue was the ambiguous wording of the original problem statement — it didn't make clear that Monty always opened a door, the door he chose never contained the prize, and Monty always offered the option to switch.
Most of these 10,000 correspondents objected without first thinking the problem through, while others thought it through and came to a mistaken conclusion. What is astonishing is that, before voicing their objection, each of these correspondents could (in principle) have written a computer model of the system and discovered their error. Such a model is included with this article, in the Resources section. (The irony is that most people don't see the correct answer to this problem, but a computer, being perfectly stupid and literal, sees it right away.)
Again, this is a Platonic math problem that only coincidentally has a real-world expression. Notwithstanding its distance from nature, it makes an unambiguous claim and is subject to falsification through experiment, therefore it is scientific. Contrary to the position taken by the second of my correspondents above, it is testable and formally inductive — it is a general statement about a class of similar problems.
Let's move away from examples of laborious, sometimes inelegant experiments into a more powerful property of mathematics: the possibility of formal proof. In everyday earthly science, because of the eternal possibility of new evidence contradicting old, a theory can only be proven false, never true. Some theories come to be regarded as very likely, but none of them is ever pronounced "true," at least not in science.
Mathematical proof stands as an exception to this rule. In Platonic mathematics, because of its separation from nature, it's possible to construct an argument that has the widest possible generality — it applies to the entire set it makes a statement about. For example, a suitably constructed assertion about particular numbers might apply to all numbers:
- A natural or counting number is a non-negative integer, a member of the set {0,1,2,3, ...}.
- A prime number is a natural number divisible only by itself and 1.
- A composite number is a non-prime natural number that is composed of primes (65535 = 3 * 5 * 17 * 257).
- All natural numbers greater than 1 are either themselves prime, or are composed of primes (this is called the fundamental theorem of arithmetic).
This is a mere statement, not a proof, but for our purposes it may stand in for one or more proofs. A proof in mathematics has no corollary in the ordinary sciences, because theories about nature are held hostage by nature and by the prospect of new evidence. But mathematics and the other sciences have a great deal in common, for example all have the property of falsifiability. I might assert that all primes are odd numbers, but this is easily falsified by 2, the only even prime. There is only one even prime, but one is not none and my claim is therefore falsified. (Also consider that without 2 in the set of primes there would be no even composites.)
I have only touched the subject of mathematical proof without elaboration, but it's important to understand this distinction between mathematics and the other sciences — in mathematics, you can construct a true or false statement, while in other sciences you can only construct statements that are either probably true or definitely false.

Mapmakers have long thought that four colors are all that is necessary to color a map so that no adjacent map regions share the same color, but this idea wasn't actually tested until the computer era. The reason is the problem isn't easily resolved by formal mathematical proof, instead it might in principle be attacked by simply testing each possible case.
In 1976 this principle was reduced to practice by Kenneth Appel and Wolfgang Haken at the University of Illinois, who constructed an elaborate computer program meant to test each case (in a set of 1,476 possible configurations). Many workers in the field of topology dislike this proof because of its complexity and inelegance, but it seems to be correct. More to the point of this article, this is an example of a finite-domain theory being confirmed by experiment, where both theory and evidence live in the Platonic domain.
This is actually a very old theorem (strictly speaking, before proof it was a conjecture), known to the ancient Greeks (appearing in a textbook by Diophantus). It goes like this:
For numbers n greater than 2, the equation:an + bn = cn
has no solutions in nonzero integers a, b and c.
By writing a perplexing note in the margin of a textbook, Pierre de Fermat made this theorem his own. Here is Fermat's note (translated from the Latin):
"It is impossible to separate a cube into two cubes, or a fourth power into two fourth powers, or in general, any power higher than the second into two like powers. I have discovered a truly marvellous proof of this, which this margin is too narrow to contain."Fermat's Last Theorem has a storied history. Because of its simple statement coupled with the difficulty of solution, it has probably created more false proofs than any other mathematical idea. According to a story, the Theorem attracted so many amateur mathematicians and useless correspondence that a university created a form letter for replies, saying:
Thank you for your submission of a proof of Fermat's Last Theorem. The first error in the proof can be found on line ____ of page ____. Sincerely,In early attempts to prove this theorem, many workers attacked it piecemeal (reminiscent of the four-color map theorem), proving it for specific exponents or ranges of exponents, but without attempting to construct a general proof. Finally, in 1993 Andrew Wiles solved the problem with an unconventional approach involving elliptic curves. After a few corrections, his result has come to be regarded as a formal proof of the Theorem.
In this case as with the others, a conjecture is made (equivalent to a hypothesis in normal science), evidence is gathered and tested, and a solution is produced that must survive the most detailed scrutiny. Unlike normal science, a formal mathematical proof answers a conjecture in a conclusive way, without the possibility of later refutation, although in some cases a more elegant, shorter proof may supersede an earlier approach on aesthetic grounds.
The Mathematics of Nature
We now turn to what many scientists regard as the language of nature, the sort of mathematics we use to describe the natural world. Nobel Prizewinner Richard Feynman had this to say about mathematics:
To those who do not know mathematics it is difficult to get across a real feeling as to the beauty, the deepest beauty, of nature ... If you want to learn about nature, to appreciate nature, it is necessary to understand the language that she speaks in.As we learn more about nature, it becomes increasingly apparent that an accurate statement about nature is necessarily mathematical. Anything else is an approximation.
A Plague of Prime Numbers

Physicist Eugene Wigner once wrote an article named "The Unreasonable Effectiveness of Mathematics in the Natural Sciences" in which he makes some of the same points I am making here. In his article Wigner says "... mathematical concepts turn up in entirely unexpected connections." This is an example of such an unexpected connection.
It is well-established that plagues of locusts (actually cicadas) historically reappear in huge swarms on either 13-year or 17-year cycles. This has been known for centuries, but until recently no one understood the reason — it was thought to be a simple coincidence.
But the numbers 13 and 17 have something in common — they are both prime numbers. Is this a coincidence, or does this reappearance interval confer a survival advantage? Let's think about this:
- The cicadas who survive do so by evolving toward an optimal survival strategy.
- One strategy would be for a lot of cicadas to appear at once, so the predators are overwhelmed by their sheer numbers.
- Another strategy would be to appear during years when there are fewer predators to attack them.
The third strategy is easier said than done, considering all the species of birds, lizards and other creatures poised to eat the cicadas. Maybe there is a strategy that minimizes predator risk no matter who the predators are or what strategy they adopt. Is that even possible?
Well, as it turns out, yes, there is a strategy. To understand it we need to know something about numbers and their possible divisors. Let's say that b represents the reproductive cycle of some predator in years, and a represents the reproductive cycle of the cicada. It turns out that if b evenly divides a, then predator b is likely to appear in synchrony with the cicadas and perhaps eat them. For example, if the cicadas reappear at 12-year intervals, then any predators that reproduce on 2,3,4 and 6-year cycles will have a good chance to eat some cicadas (notice that 12 is evenly divisible by 2,3,4 and 6), so on that basis a 12-year reproductive cycle would seem to be a particularly bad choice.
Another helpful strategy is to stay in hiding for a long time between appearances, to minimize the chance of being attacked. This strategy must be balanced against the slow pace of reproduction created by spending a lot of time in hiding. A fast reproduction cycle exposes the cicada to too many attackers too often, but a slow reproductive cycle might allow the cicada to be outcompeted by creatures willing to take more risks.
And a very important point. Evolution is not a plan, it is an algorithm. Cicadas that happen to have a bad strategy simply die, and those that happen by chance to have a better strategy reproduce in greater numbers. There is no grand plan, instead there are a lot of creatures eating each other in a big, open-air experiment. Cicadas that survive might randomly change their strategy and gradually move toward an even better strategy over time, but on the basis of random mutations, not choices.
So we have a survival strategy with two parts:
- Choose a reproductive cycle time that balances risk with opportunity. A short cycle risks encountering too many predators. A long cycle means the cicadas will be outcompeted by creatures willing to take more risks.
- Choose a specific reproductive cycle that minimizes the risk of falling into synchrony with any predator's reproductive cycle. This means choosing a cycle time that has as few divisors as possible.
What kind of number has few divisors? Well, prime numbers have no divisors except themselves and 1, so they're an obvious choice. Interestingly, among reasonable year numbers, we just showed that 12 is a bad choice, but its immediate neighbors 11 and 13 are prime numbers, therefore good choices. The next prime after 13 (17) is a good choice as well, and perhaps optimal. These numbers minimize the risk of falling into synchrony with the reproductive cycles of various predators.
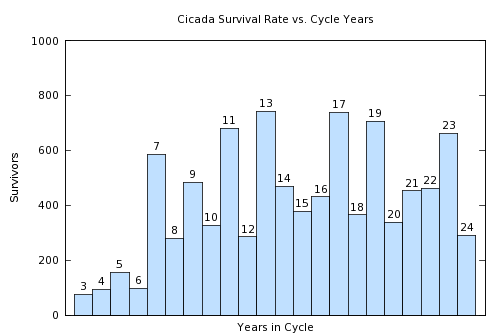 Figure 1
Figure 1Isn't a conversation like this just contentless hypothesizing, with no possibility for acquiring evidence? Well, no, in fact one can easily write a computer model that compares various survival strategies and test these ideas. I know because I did just that, and the model's result is shown as Figure 1 on this page. (The model itself is in the Resources section of this article.)
In my model I generated a large number of different reproductive cycles for cicadas and predators and compared them. Whenever predators and cicadas appeared at the same time, I let the predators eat the cicadas. The remainder of the time I allowed normal population increases. And I penalized overly long reproductive cycles, just as nature does.
My very simple computer model shows a clear advantage for reproductive cycles that are prime numbers — notice in Figure 1 that the numbers 7,11,13,17,19 and 23 (all primes) have more surviving cicadas than other numbers. Also notice that the number 12, nestled between two primes, shows a particularly bleak cicada survival rate, for the reason that 12 has a lot of divisors (e.g. encounters with predators).
It's important to understand that my simple computer model doesn't know anything about prime numbers, and neither do cicadas. All the model does is allow a cicada feast any time predators and cicadas appear at the same time. Using that simple rule, the model rewards reproductive cycles based on primes because that strategy favors the cicadas — just as in nature.
One additional note. In nature, cicadas aren't really free to choose any prime number as in my model, because to survive they need to appear in a huge swarm, also they need to meet others of their own kind in order to reproduce. So unlike this simulation, the seven real-world cicada species have evolved just two behaviors — 13-year (southern U.S.) and 17-year (northern U.S.) reproductive cycles.
This experimental result leads to several important conclusions:
- A theory about evolution in cicadas, that claims an advantage for a prime-number reproductive cycle, can be tested by writing a simple computer model.
- Even though the model and the theory behind it live in an abstract mathematical domain, they tell us something about nature.
- This example shows a classic scientific event sequence:
- Hypothesis
- Experimental design
- Experiment
- Analysis
- Conclusion
- Because this purely mathematical idea can be tested and is subject to falsification, it meets the definition of a scientific theory.
- This example shows the degree to which natural phenomena only make sense to someone who understands mathematics.
- It seems Richard Feynman was right — nature speaks to us in mathematics.

When mathematical physicist Paul Dirac was asked what he believed, without hesitation he replied that the laws of nature should be expressed in beautiful equations. This is a story of one of the more beautiful convergences of mathematics and nature, one that vindicated Dirac's belief and won him a unique place in the history of both physics and mathematics.
To put this in perspective, I need to describe the quantum world. Physics at a large scale is made up of continuous quantities — you can measure a meter, or a millimeter, or a micrometer, and all these measurements have meaning and can be added up. But at a very small scale, the universe acts differently. To give a sense of this microscopic world, let's use this thought experiment:
- Let's say that individual atoms are coins that can only have two states — "heads" or "tails."
- Let's say further that an atom that is "heads" has a value of one and "tails" has a value of zero.
- Nature flips the atoms in a completely unbiased way, so a large collection of atoms has an average value very likely to be near 1/2.
- Even though a large collection of atoms should have an average value near 1/2, a small, random probability exists for values other than 1/2, which means quantum effects can sometimes influence the macroscopic world.
- Nature randomly flips the atoms, at times and places of her own choosing, and we cannot discover which atoms nature has flipped until we examine them.
- At a large scale, we can rely on an object being the same from moment to moment, but as we magnify the picture, we eventually get to a scale at which matter isn't continuous, but is broken up into little packets of matter and energy — "quanta" — whose state depends on rules of probability.
I emphasize that this thought experiment is greatly simplified and is meant only to give a sense of the quantum world.
Because of the discontinuous nature of quantum theory, it seems the large-scale (macroscopic) and quantum worlds operate on different principles — I can have a kilogram of uranium, or a gram, or a tiny mote, but I will eventually get to a point at which I can't measure the uranium on a continuous scale, and more important, I can't be sure the uranium will behave according to classical rules — at a random time it might turn into something else, like lead.
The physicists who studied the quantum world created a new theory to describe reality at this scale. Quantum theory is based on probability and is discontinuous at small scales of space, time, mass and energy. In spite of the built-in uncertainties, the quantum theory is very successful at predicting certain aspects of the world around us, and most of modern technology derives from our understanding of quantum theory.
Because of quantum theory we now have two kinds of physical theories — those that work at a large scale, and those that work at the scale of individual atoms. Unfortunately for physics, these theories are incompatible — the very successful theory of relativity isn't expressible in quantum terms, and vice versa. When you read about the search for a "unified" physical theory, this is the reason — our present theories conflict with each other, and we are now seeking a more complete theory to resolve the conflicts.
 Paul Dirac
Paul DiracEven though we don't have a unified theory that works at all scales, physicists have discovered elements of such a theory. One of these elements is an equation written by Paul Dirac in 1928. Dirac's equation successfully predicts the behavior of particles moving at relativistic velocities, so to some degree it reconciles the relativistic and quantum views of reality.
In 1933 Dirac won a Nobel Prize for his work, and while delivering his acceptance speech he revealed an interesting side effect of his equation. To put Dirac's revelation in its simplest terms, let's use this equation:
(1)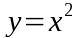
If we solve equation (1) for x, we get:
(2)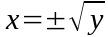
What does "±" mean? In mathematics it means there are two solutions to the equation, one positive and one negative. This follows from the fact that:
(3)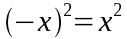
To say this another way, when we square a variable we throw away the sign of the original value, and if we rewrite the equation, we must remember to acknowledge the two possible signs (or roots).
While writing his equation Dirac realized it had two possible roots. At that point, Dirac could have decided his equation was only an approximation of reality (there are plenty of those), or he could claim his equation accurately described nature, therefore nature allowed two different kinds of matter, with positive and negative signs. Dirac decided his equation described nature.
Wasn't this arrogant behavior? Isn't it more likely that an equation is just a weak imitation of nature and likely to include absurd possibilities? Yes, that sometimes happens, but the history of science teaches us that, overall, equations tend to reflect nature in direct proportion to their beauty and simplicity. Dirac realized he could rewrite his equation to eliminate the negative root, but that equation would have been complex and unattractive, solely to eliminate the strange possibility that nature allowed two kinds of matter. Acting primarily on instinct, Dirac decided his equation accurately reflected nature, and he described the possibility of something he called "antimatter."Dirac's antimatter idea was first regarded as a weak hypothesis or an alternate universe that could not coexist with this one (since matter and antimatter don't get along very well). But within a few years antimatter had been observed. In 1932 Carl Anderson, a young physicist at the California Institute of Technology, was observing cosmic rays pass through a cloud chamber. To his astonishment he observed the passage of "something positively charged, and with the same mass as an electron." Unsure of his conclusion he continued observing until he had enough data to be certain — he had discovered a particle like an electron, but with a positive charge (normal electrons have a negative charge). The particle, now called a "positron," was the first experimental confirmation of Dirac's antimatter — his instincts had served him well.
Conclusion
Let me ask a question. Did Dirac invent his equation, or did he discover it? If we claim he invented it, because nature subsequently obeyed Dirac's equation and in ways no one could have expected, this must make Dirac God. But Dirac isn't God, therefore he discovered his equation. If Dirac discovered his equation, where did he find it? He found it in nature. For the entire history of the universe, Dirac's equation lay as an undiscovered treasure in the bosom of nature, until Dirac happened upon it.
Conclusion? Nature is innately mathematical, and she speaks to us in mathematics. We only have to listen.
Because nature is mathematical, any science that intends to describe nature is completely dependent on mathematics. It is impossible to overemphasize this point, and it is why Carl Friedrich Gauss called mathematics "the queen of the sciences."
I decided to write this article after debating psychologists about the low scientific standing of their field. During these conversations it became apparent that many psychologists don't understand or have any use for mathematics and may not even recognize it as science. In a field like psychology, one that believes itself to be scientific, this level of ignorance represents a profound and crippling disconnect, and for individual psychologists to try to explain why mathematics isn't scientific can only reveal an astonishing degree of narcissism and arrogance.
This degree of mathematical ignorance, which in my experience is typical of clinical psychologists, eloquently answers the question raised by my article "Is Psychology a Science?." I found that the psychologists who felt justified in questioning the scientific standing of mathematics were in fact incompetent either to describe or explain it, and in my view they would have been better off learning the topic before expounding on it. As to the reverse case, after debating psychologists for several years, I think I can describe them in some limited ways, but I have no chance of explaining them.
A closing thought. Please submit this article — I think it deserves to be widely read.
Resources
First, please click this link for a rather funny cartoon on this article's topic. Randall Munroe is a pretty funny guy, but what sets him apart is that his cartoons provoke thought.
Next, I wrote a number of computer programs in support of the research that led to this article. This section provides the programs and describes their use. They are all written in Ruby (easily rewritten in other languages), and some of them assume a Linux platform for particular behaviors or results (but none of them require a Linux platform). To use these programs, download them, remove the ".txt" suffix, and make them executable.
Euler's Prime Function
This Ruby program tests Euler's Prime Function. For tutorial reasons it is written as though the outcome is not certain, then proclaims "Hypothesis falsified" at the end of its run. Note the inefficient prime testing function — in a faster, more efficient program of this kind, one would write a Sieve of Eratosthenes.The Monty Hall Problem
This Ruby program compares the two cases of the Monty Hall Problem (the cases where the contestant doesn't, and does, switch doors). The output will look something like this (it differs from run to run because pseudorandom numbers are used):
Monty Hall Problem: Switching doors: win probability 0.66723 Not switching doors: win probability 0.33286The discrepancy between these results and the canonical probability results of 2/3 and 1/3 respectively, is due to finite floating-point resolution and limited sample size.
A Plague of Prime Numbers
This Ruby program models the environmental interaction between cicadas and predators. It is a simple model that leaves out a number of real-world factors that are difficult to simulate but that don't affect the broad result.
In development I tested an exponential growth strategy, but this created unrealistic results in which the sole outcome was a single prime number period, unlike what is seen in nature. Because real environments have limited exploitable resources, a model that adds and subtracts members turns out to be more realistic than one in which the population is multiplied by a growth rate factor on each round.
This model also penalizes long reproductive cycle rates, assuming that the longer the cicadas lie dormant, the more likely they will fall prey to drought, flood, fire, and predators willing to dig them up, or be outcompeted by faster-reproducing species.
The program creates a simple text histogram for testing purposes, and it also creates a nice-looking plot of its results (seen in the main body of this article) if your system happens to have "gnuplot" installed.
Feedback
| Home | | Mathematics | | * Is Mathematics a Science? | |  Share This Page Share This Page |