 Share This Page
Share This Page| Home | | Science | | * Gravity | |  Share This Page Share This Page |
Exploring the interplay of gravity and mass-energy
— P. Lutus — Message Page —
Copyright © 2017, P. Lutus
Most recent revision:
(double-click any word to see its definition)
In this article we'll explore the relationship between gravity and energy, and consider some consequences for matters both large and small. This article uses animations and graphics to clarify its points, and some key equations are included and explained. Finally, we'll discuss a new theory about the universe — how it might have come into being without either violating any laws of physics or requiring supernatural intervention.
The overview:
Power and Energy
Notice the minus sign in equation (4) above — it means that gravitational potential energy is negative. Because this is an important property with cosmological significance, I would like to explain how it comes about.
The reader may recall my earlier remark than energy is the time integral of power, but this is just one example — in mechanics, work ($W$) can be expressed as the integral of force ($f$) with respect to distance ($x$) rather than time:
\begin{equation} W = \int_a^b f dx = f x \end{equation}Expressed in everyday language, work is equal to force times distance. Now we'll apply this to gravitation — here is the force equation ($f$) for gravitational attraction between two masses $m_1$ and $m_2$, separated by a distance $r$, and under the influence of the gravitational constant term $G$:
\begin{equation} f = G \frac{m_1 m_2}{r} \end{equation}Equation (6) is the classic expression of Newton's Law of Universal Gravitation. To move from force to energy, we need to integrate equation (6) with respect to distance ($r$):
\begin{equation} E_p \int G \frac{m_1 m_2}{r} dr = -G \frac{m_1 m_2}{r} \end{equation}Equation (7) tell us that negative gravitational potential energy is the correct physical interpretation, and it arises from mathematics, not an arbitrary choice or convention.
One more thing — under General Relativity, gravity is not a force, instead it arises as a result of spacetime curvature. But in ordinary circumstances the Newtonian conventions still apply, and energy is still a meaningful concept in orbital mechanics.
NOTE: If the animations in this section distract the reader, one may click them to make them stop.
Remember that mass-energy cannot be created or destroyed, only changed in form. A more general way to say this is that the universe has a constant quantity $Q$ of mass-energy, fixed at the moment of the Big Bang and unchanged since. We'll be discussing the quantity $Q$ throughout this paper, and we'll eventually assign it a value.
(Click below to start or stop the animation)
Kinetic Energy $E_k$:
Potential Energy $E_p$:
Total Energy $E_t$ ($E_p+E_k$):
0.0
0.0
0.0
Figure 2: Pendulum Energy Model
(Click the image to start/stop the animation.)
Pendulum
As a mass moves in a gravitational field, it typically exchanges kinetic and potential energy. A swinging pendulum (Figure 2) has maximum kinetic energy at the lowest point in its swing, and zero kinetic energy at the highest. The pendulum's potential energy has the reverse relationship — it increases (i.e. becomes less negative) with distance from the center of the earth, and in exchange, the kinetic energy must decrease. The important thing to understand about freely moving objects in a gravitational field is that their energy, the sum of kinetic and potential energy, is constant.
There is a well-known principle in mechanics called Newton's First Law which says that, unless acted on by an external force, an object will maintain a constant state of motion. There is, or should be, a corollary for freely moving objects in space:
Unless acted on by an external force, an object moving in space will maintain a constant energy.
This doesn't mean the object's velocity will remain the same, nor does it mean the object's kinetic and potential energy values will remain the same. It means the total energy, the sum of kinetic and potential energy, will remain the same.
The swinging pendulum in Figure 2 shows this — even though there is a periodic exchange between kinetic and potential energy, the total energy ($E_p + E_k$) is constant. If our pendulum were located in a vacuum and had lossless bearings, it would continue to swing forever in the same way, perpetually conserving its energy.
For small-scale mechanical systems like the pendulum, it's convenient to establish an arbitrary zero point for potential energy. In this case, the zero point is set at the bottom of the swing, so potential energy is pictured as increasing from zero to positive values as the pendulum swings. This is a reasonable way to picture a physical system, but the absolute value of gravitational potential energy is typically a much larger value, and is always negative.
Satellite
Pendulums don't usually get to swing in a vacuum with frictionless bearings, but an orbiting satellite is a better example of a frictionless system. Like the pendulum, as the satellite orbits it carries both kinetic and potential energy:
Here again are the equations for kinetic and potential energy ($E_k$ and $E_p$), and a derived equation for total orbital energy ($E_t$):
\begin{equation} E_k = \frac{1}{2} m v^2 \end{equation} \begin{equation} E_p = -\frac{G m_1 m_2}{r} \end{equation} \begin{equation} E_t = \frac{m_1 r v^2 - 2 G m_1 m_2}{2 r} \end{equation}To be consistent with the Principle of Energy Conservation, for a freely orbiting body with no external forces acting on it, over time equation (10), the sum of kinetic and potential energies, produces a constant.
(Click below to start or stop the animation)
Kinetic Energy $E_k$:
Potential Energy $E_p$:
Total Energy $E_t$ ($E_p+E_k$):
0.0
0.0
0.0
Figure 3: Elliptical Orbit Energy Model
(Click the image to start/stop the animation.)
Figure 3 shows a satellite in an elliptical (oval-shaped) orbit around a central body. I chose this configuration to show that, even though there is an ongoing exchange between kinetic and potential energy, as with the pendulum the total energy remains constant. By the way, this orbital shape isn't hypothetical — comets often have highly elliptical orbits like this. Many comets dwell far beyond Pluto and only rarely descend into our neighborhood for a brief appearance. And sometimes an object approaches the solar system from afar, in a hyperbolic orbit (explained below), to then depart at high speed.
Interestingly, Johannes Kepler computed the properties of orbits and wrote what we know as Kepler's Laws of Planetary Motion, but without understanding the reason orbits behave as they do. The secret to understanding orbits is to recognize that their motion conserves energy, and if they behaved at all differently, nature would need different laws.
Now let's look at the relationship between an orbit's kinetic and potential energy. Here is an approximate equation for the velocity of a circular orbit $v_o$:
\begin{equation} v_o \approx \sqrt{\frac{m_2^2G}{(m_1 + m_2)r}} \end{equation}Where $m_1$ is the satellite's mass, $m_2$ is the central body's mass, $r$ is the orbital radius and $G$ is the universal gravitational constant. If the satellite is much less massive than the central body, this simpler approximate equation may be used:
\begin{equation} v_o \approx \sqrt{\frac{G M}{r}} \end{equation}Where $M$ is the central mass, $r$ is the orbital radius and $G$ is the universal gravitational constant. It turns out that, for circular orbits, the relationship between kinetic and potential energy is fixed, regardless of the orbit's other properties — the negative gravitational potential energy is always twice the magnitude of the positive kinetic energy. Another way to say this is that, for a circular orbit, 2/3 of the energy is negative potential and 1/3 is positive kinetic.
In each of the cases examined so far — the pendulum as well as the elliptical and circular orbits — the sum of energies has been negative, dominated by negative gravitational potential energy. Obviously we might select a very high velocity and produce a positive result for equation (10) above, the total orbital energy. But is there an orbital velocity that exactly balances the two kinds of energy and produces zero? Yes, there is — it's called escape velocity. Here is its value, using the terminology from the previous section:
\begin{equation} v_e = \sqrt{\frac{2 G M}{r}} \end{equation}Escape velocity has some interesting properties. If an object is propelled away from an airless planet with an initial impulse of escape velocity (sort of like Alan Shepard's famous golf shot on the moon, but a much higher velocity), that object will continue to move away, at gradually decreasing speed, but it will never stop and return. In fact, at an infinite distance, an escape-velocity object will achieve zero velocity. Here are the properties of an object initially given escape velocity:
There are two canonical orbital velocities — one is the circular velocity $v_o$ provided by equations (11) or (12), the other is escape velocity $v_e$ provided by equation (13). Velocities greater than escape velocity $v_e$ or less than circular velocity $v_o$ produce interesting effects, like the large family of elliptical orbits resulting from initial velocities in the range 0 < v < $v_o$ and shown in Figure 3 above. But because escape velocity has properties of cosmological significance, it merits a closer look.
Because of its importance to what follows, we should prove that escape velocity results in zero net energy (i.e. $E_k$ + $E_p$ = 0). First, let's simplify equation (10) — let's normalize the mass of the orbiting body $m_1$ to 1. Here is the result:
\begin{equation} E_t = \frac{r v^2 - 2 G M}{2 r} \end{equation}Remember that equation (14) provides the total energy of an orbiting body, the sum of positive kinetic and negative potential energy. At this point, those sufficiently adept at mathematics will compare equations (13) (escape velocity) and (14) (total energy) and a light bulb will go off. For the rest of us, here's a step-by-step proof:
\begin{equation} E_t = \frac{r v_e^2 - 2 G M}{2 r} = \frac{r \sqrt{\frac{2 G M}{r}}^2 - 2 G M}{2 r} = \frac{r \frac{2 G M}{r} - 2 G M}{2 r} = \frac{2 G M - 2 G M}{2 r} = 0 \end{equation}Q.E.D. An object given escape velocity will have zero orbital energy, and very important, this is only true at escape velocity, no other.
To summarize:
Big Bang
When Georges Lemaître first proposed the Big Bang theory, there were a number of objections — at the time there was no evidence in support of the idea, it seemed counterintuitive, and it appeared to violate basic physical principles. How could the universe arise out of nothing?
But over the years, evidence has begun to accumulate that the Big Bang may be real:
All this evidence has given the Big Bang the status of a scientific theory, that is to say, a theory supported by evidence and falsifiable in principle. But one objection to the Big Bang remains, and it is serious — there is no physical law so well-established as the conservation of mass-energy, and the Big Bang seems to violate it. By creating an entire universe of mass-energy out of nothing, the Big Bang seems to break the most basic rule of physics: no free lunch.
But this final objection is answered by the idea expressed in this article — if the universe began with an exact balance between positive mass-energy and negative gravitational potential energy, the law of mass-energy conservation is honored.
For this condition to be met, the Big Bang would have to create the universe with an exact balance between positive mass-energy and negative gravitational potential energy, so the total mass-energy is equal to zero. Therefore the Big Bang would have to give matter an initial velocity exactly equal to escape velocity. Is there any evidence for this? In a word, yes.
It turns out there is a relationship between the average velocity of matter in the expanding universe, and the overall curvature of spacetime. Since the beginning of Big Bang cosmology, the spacetime curvature issue has been much studied, with three likely outcomes:
Terms:
- $\Omega$ = Mass-energy density parameter
- $Q$ = Sum of positive kinetic energy and negative gravitational energy.
- $V$ = Expansion velocity, normalized to escape velocity $v_e$.
- $\theta$ = Sum of a triangle's inner angles.
Parameters
$Q \lt 0$
$V \lt v_e$
$\theta \gt 180^{\circ}$Expansion velocity is less than escape velocity, negative gravitational energy predominates, space is positively curved, expansion will reverse and the universe will eventually collapse. 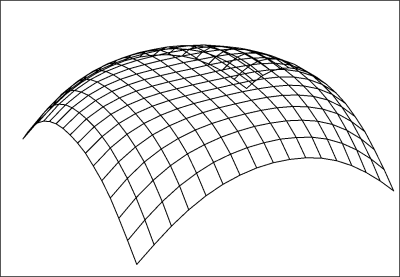
$Q = 0$
$V = v_e$
$\theta = 180^{\circ}$Expansion velocity is equal to escape velocity, total energy is equal to zero, space is flat or classically Cartesian, expansion velocity will decrease asymptotically and reach zero at infinity. 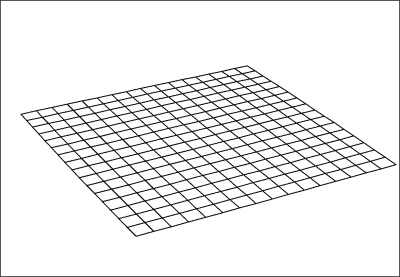
$Q \gt 0$
$V \gt v_e$
$\theta \lt 180^{\circ}$Expansion velocity is greater than escape velocity, positive mass-energy predominates, space is negatively curved, expansion will not approach zero at infinity. 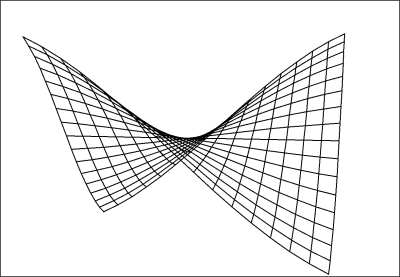
I emphasize that the above table summarizes conditions near the time of the Big Bang. The recent discovery of Dark Energy as an acceleration term in universal expansion doesn't change the physics for that era because positive mass-energy and negative gravitational energy were both much larger factors than dark energy.
The above table suggests that, if space is classically flat or Cartesian, this supports the zero-energy condition required for the Big Bang to create the universe without violating energy conservation. And there is good evidence that space is flat. This doesn't mean there isn't local strong curvature near masses, it means the overall large-scale curvature of spacetime is flat.
Quantum Uncertainty
It has been recently suggested that, if the Big Bang could impart escape velocity to the universe's matter — thus balancing positive and negative energy — a random quantum fluctuation could have brought the universe into existence. To those unfamiliar with quantum ideas this may seem absurd — aren't quantum effects limited to extremely small scales?
Well, no — quantum effects are a matter of probability, not possibility. On a microscopic scale, quantum effects are routine and must be taken into account on a moment-to-moment basis. But there's no "quantum barrier" that separates large-scale reality from the microscopic scale. It is a simple matter of statistics — the probability of a macroscopic quantum effect is inversely proportional to the mass under consideration. Consider this expression:
\begin{equation} \Delta x \Delta p > \frac{\hbar}{2} \end{equation} Where:The above relation, known as Heisenberg's Uncertainly Principle, describes the role of uncertainly in quantum theory. Instead of denying the possibility of large-scale quantum effects, this principle gives them a probability estimate. And the outcome is that, for large masses, one might have to wait a very long time to see a manifestation of quantum uncertainly at a macroscopic scale — maybe even a billion years. But a billion years seems like reasonable time to wait for a universe.
"Because there is a law such as gravity, the universe can and will create itself from nothing ... Spontaneous creation is the reason there is something rather than nothing, why the universe exists, why we exist." — Stephen Hawking in "The Grand Design".
In October 2017 this article was extensively reworked (same content, new presentation). Because of the abandonment of Java in Web pages, the Java demonstration applets were replaced by JavaScript. All equation renderings, originally graphic images, were replaced by Latex content rendered by the MathJax engine. Much better overall appearance, and the demonstration animations function once again.
| Home | | Science | | * Gravity | |  Share This Page Share This Page |