We now turn to an interesting differential equation that has many applications. Its simplicity of expression belies its wide application in various branches of physics. It has several versions, we will examine two.

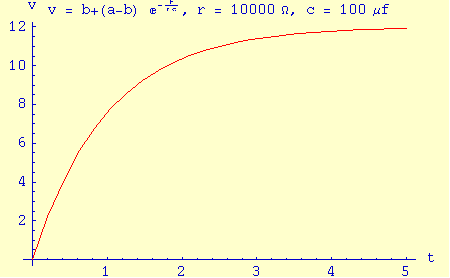
Voltage at capacitor in series RC circuit.

Version 1:

(1)  y(t) + r c y'(t) = b
(2)  y(0) = a

The solution for these terms is:

(3)  y(t) = b + (a-b) e^-t/rc

Where e represents the base of natural logarithms. This equation describes how a quantity (temperature, water, gas, electricity) changes from one value to another (from a to b). On careful examination of the differential equation terms, one can see that the rate of change is proportional to the remaining distance, e.g. as the goal is approached, the rate declines. As it turns out, this equation applies to an amazing number of situations, of which this is just a short list:

• In an electronic RC circuit, it describes the rate at which a capacitor charges. In this case, the terms r and c mean resistance and capacitance. See the example graph on this page.
• In a thermally coupled system consisting of a hot and cold body, this equation describes how rapidly the cold body warms up to the temperature of the warm one (assuming the warm body to be much larger than the cold one). In this case, c refers to the mass of the cold body and r refers to the reciprocal of thermal conductivity between the bodies.
• In a system consisting of two connected gas reservoirs at different pressures, this equation described how the two reservoirs come to the same pressure (again, one of the reservoirs is thought to be much larger than the other). In this case, c refers to the capacity of the smaller reservoir and r refers to the resistance to gas flow on the path that connects them.
• In oceanography, specifically the case of a bay that is connected to an ocean by way of a channel, this equation describes the relationship between water flow through a channel versus the difference in water height. In this case, c refers to the bay's water capacity, r refers to the channel's resistance to water flow, and a-b describes the difference in height between the bay and ocean.

In several of the above listed applications (including the electronic and oceanographic examples), a different form of the equation is appropriate, one in which there is a sinusoidal driving waveform. Here is that form.

Version 2:

(4)  y(t) + r c y'(t) = m sin(ω t)

The new terms are: m = the magnitude of the driving waveform, ω = 2 π f and f = frequency of driving waveform in Hertz.

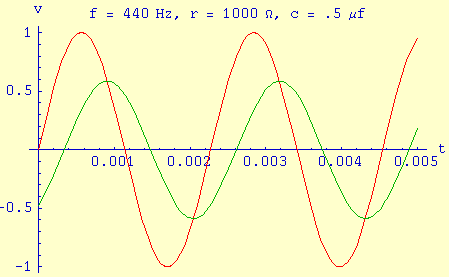
Red = source waveform. Green = waveform at capacitor in series RC circuit.

This version of the differential equation produces a continuous function with no initial values:

(5)

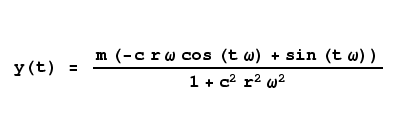
Like the form described above, this deceptively simple equation is also widely used in physics and technology to analyze periodic processes, such as the voltage and phase relationships in an electronic RC circuit (see the example on this page) as well as other fields that deal with periodic waveforms. It has even been used by the author to choose a boat departure time from a bay in Alaska. On that occasion it was important to establish the time of slack water in a channel leading from the bay to the ocean. In this case the "driving waveform" was none other than the ocean's daily tidal cycle.