Home | Mathematics |     Share This Page
Trigonometric Relations

A concise summary of trigonometric equations.

Copyright © 2009, Paul Lutus — Message Page

 
Right Triangle Element Names:
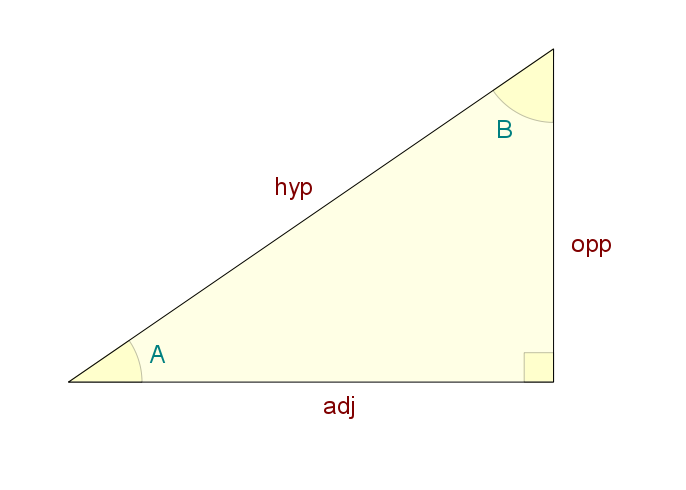
Relationship Matrix (angles in radians):

Want

H
a
v
e

  
 
opp
adj
hyp
A
B
opp & adj — — $ \displaystyle \sqrt{opp^2+adj^2}$ $ \displaystyle \tan^{-1}(\frac{opp}{adj})$ $ \displaystyle \tan^{-1}(\frac{adj}{opp})$
opp & hyp — $ \displaystyle \sqrt{hyp^2-opp^2}$ — $ \displaystyle \sin^{-1}(\frac{opp}{hyp})$ $ \displaystyle \cos^{-1}(\frac{opp}{hyp})$
adj & hyp $ \displaystyle \sqrt{hyp^2-adj^2}$ — — $ \displaystyle \cos^{-1}(\frac{adj}{hyp})$ $ \displaystyle \sin^{-1}(\frac{adj}{hyp})$
opp & A — $ \displaystyle \frac{opp}{\tan(A)}$ $ \displaystyle \frac{opp}{\sin(A)}$ — $ \displaystyle \frac{\pi}{2} - A$
opp & B — $ \displaystyle opp \, \tan(B)$ $ \displaystyle \frac{opp}{\cos(B)}$ $ \displaystyle \frac{\pi}{2} - B$ —
adj & A $ \displaystyle adj \, \tan(A)$ — $ \displaystyle \frac{adj}{\cos(A)}$ — $ \displaystyle \frac{\pi}{2} - A$
adj & B $ \displaystyle \frac{adj}{\tan(B)}$ — $ \displaystyle \frac{adj}{\sin(B)}$ $ \displaystyle \frac{\pi}{2} - B$ —
hyp & A $ \displaystyle hyp \, \sin(A)$ $ \displaystyle hyp \, \cos(A)$ — — $ \displaystyle \frac{\pi}{2} - A$
hyp & B $ \displaystyle hyp \, \cos(B)$ $ \displaystyle hyp \, \sin(B)$ — $ \displaystyle \frac{\pi}{2} - B$ —

Notes:

  • $ \displaystyle \frac{\pi}{2} \text{radians} = 90^{\circ}$

  • $ \displaystyle \sin(A) = \frac{opp}{hyp}$

  • $ \displaystyle \cos(A) = \frac{adj}{hyp}$

  • $ \displaystyle \tan(A) = \frac{opp}{adj}$

  • $ \displaystyle \sin(B) = \frac{adj}{hyp}$

  • $ \displaystyle \cos(B) = \frac{opp}{hyp}$

  • $ \displaystyle \tan(B) = \frac{adj}{opp}$

References:

Home | Mathematics |     Share This Page