

 Share This Page
Share This Page| Home | | Science | | * Dark Energy | |  |  |  Share This Page Share This Page |
(double-click any word to see its definition)
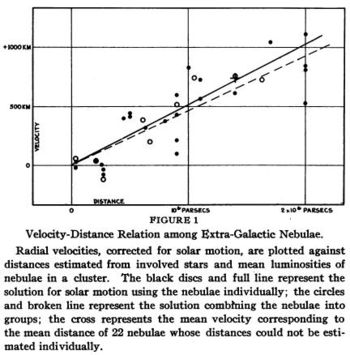
In 1929, using new, much better telescopes than had existed before, astronomer Edwin Hubble discovered that distant "extra-galactic nebulae" appeared to be receding, and he showed that their rate of recession was proportional to their distance. Over time several things became clear:
George Gamow first suggested this cataclysmic scenario, and in a back-of-the-envelope calculation, he produced an estimate of the original explosion temperature and a residual temperature resulting from the subsequent universal expansion (he guessed it would be around 5 Kelvins, which would be easily measurable in the microwave spectrum).
A few years later Arno Penzias and Robert Wilson were working on an unrelated problem with a very sensitive microwave antenna at Bell Labs. They found an annoying noise signal they could neither identify nor eliminate. While reading the literature of the time, they happened on a preprint of an article that suggested that Gamow's Big Bang afterglow might be detectable with a sufficiently sensitive microwave antenna.
Dear reader, please imagine this. There's a group of researchers at Princeton University who have a theory but no antenna, and another group at Bell Labs who have an antenna but no theory. The group at Princeton are busy writing grant applications, trying to gain access to a suitable antenna, while the Bell Labs people are crawling around in a huge, perfectly suitable antenna, scrubbing away some bird droppings they think might be the source of that annoying noise. If I wrote this as fiction, no one would believe it.
But, contrary to all expectation and experience in this highly competitive field, the two groups managed to make contact, coöperated in making the required measurements, and published their results ... jointly. Penzias and Wilson later won the Nobel Prize for this work.
The Big Bang theory gradually came to to be well-supported by observation, and this led to a discussion of the overall shape of the universe, a topic intimately tied to expansion velocity and mass density.
Once the expansion of the universe became accepted, observations began to try to establish at what rate it was expanding. Cosmologists realized if they could establish two key facts, the mass density and the expansion rate, they could make a prediction about the future of the universe. They realized if the universe's expansion velocity lay below a certain critical value, the universe would eventually collapse (and perhaps expand all over again). If the velocity lay above that critical value, the universe would expand forever.
This question is based on the same principle as escape velocity. If a rocket can achieve a certain speed, it can escape Earth's gravitational pull and escape. If it doesn't achieve that critical velocity, it will fall back to Earth. At a certain velocity, the rocket will orbit the Earth, without either escaping or falling back.
In the cosmological version of this question, knowledge of the expansion velocity and the mass density determines the geometry, or the curvature, of space itself. Cosmologists use the term density parameter to describe this trait. If the density parameter is less than one, space has negative curvature and the universe will expand forever — it can be said to have "escape velocity." If the density parameter is greater than one, the universe has positive curvature and the universe will eventually collapse back to a point (a Big Bang in reverse). Here is a pictorial description of the three outcomes:
|
Density Parameter (Ω)
|
Description
|
Graphic (click images for 3D)
|
|
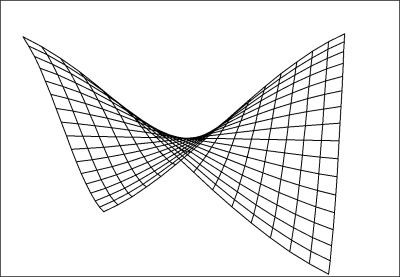
Ω < 1.0
|
Expansion velocity is greater than mass density, space is negatively curved (the inner angles of a triangle sum to less than 180°), expansion will continue forever. |
|
|
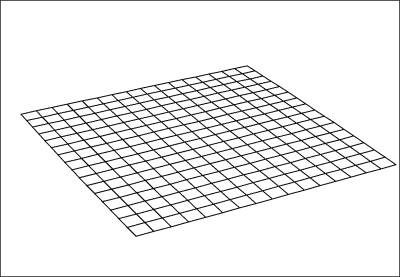
Ω = 1.0
|
Expansion velocity is matched with mass density, space is flat or classically Cartesian (the inner angles of a triangle sum to exactly 180°), expansion velocity will slowly decrease, but the universe will neither expand without bound, nor will it collapse. |
|
|
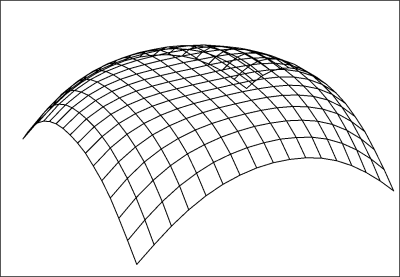
Ω > 1.0
|
Expansion velocity is less than mass density, space is positively curved (the inner angles of a triangle sum to greater than 180°), expansion will reverse and the universe will eventually collapse. |
|
This problem occupied cosmologists for many years, and astronomers did all they could to provide better measurements for both mass density and expansion velocity. Implicit in this work was the assumption that the universe obeyed the same relatively simple laws in all locations, and for all time.
This assumption has turned out to be false. Today physics is in a position much like that created by the failure of the Michelson-Morley experiment.
| Home | | Science | | * Dark Energy | |  |  |  Share This Page Share This Page |